SVM 数学推导及应用

SVM可以说是分类算法中效果最好的算法之一了，我与SVM结缘于2011年(☺)，当时导师的一个项目需要对有标注的文本分类，就搞了一下SVM(其实是导师让我搞一下)。当时还没上研究生，很多东西不得要领，就使用了cjlin老师的libsvm，但一直想把相关数学搞明白，后来由于种种原因岁月蹉跎，直到最近才把这块完成，也算是有始有终，SVM数学推论较多，我尽量在简单的前提下把来龙去脉讲清楚。

先上数学吧，搞懂数学才能搞懂算法，假设数据线性可分，则必可以求出一个超平面将数据分开。那SVM求的是这样的一个超平面H：将H平移得到两个超平面H1和H2，使离H最近的正负样本刚好分别落在H1和H2上，H1到H2之间的距离定义为Margin，SVM目的就是最大化该Margin，如图所示：

支持向量

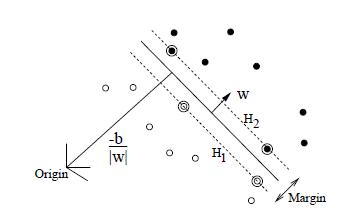
上图中的实线超平面就是所求的H，虚线超平面H1和H2之间的距离就是Margin，而落在H1和H2上的空心和实心样本点就叫做支持向量，故而名为支持向量机，为啥取了一个这么怪的名字，后面会说到。

即可定义为：存在数据 $\{x_i,y_i\} , i=1,2,3...m, y_i\in\{-1,1\}, x_i\in R^d$ ，有一个超平面H $w\cdot x+b = 0$ 可以将数据分开来，则H1和H2可以表示为： $\{w\cdot x+b = 1 \\w\cdot x+b = -1$ ，因为值域为-1和1。则除了支持向量在这两个超平面之上外，其余的点都满足 $\{w\cdot x_i+b \ge 1, \ for\ \ \ y_i=1 \\w\cdot x_i+b \le -1,\ for\ \ \ y_i=-1$ ，可以写为： $y_i(w\cdot x_i+b) -1 \ge0$ ，而需要最大化的Margin可以表示为(平行平面间距离)： $\max Margin = \max \frac {2}{||w||}$

综上，最大化Margin的公式可以转化为如下的条件极值问题(最大化中 $||w||$ 作为分母，即最小化 $||w||$ ，加上了平方和参数，是为了方便求解，但不影响极值问题)：

$\{\qquad \qquad \qquad \qquad \min {\frac{1}{2}||w||^2} \\ s.t. \qquad \qquad \qquad y_i(w\cdot x_i+b) -1 \ge0$

再根据拉格朗日法，推论参见，原问题变为： $\{ L(w,b,\alpha_i)=\frac{1}{2}||w||^2-\sum_{i=1}^{m}{\alpha_i(y_i(w\cdot x_i +b )-1)} \\ \alpha_i \ge 0$

注意观察，重要的地方要来了，现在 $\max_{\alpha_i \ge 0} L(w,b,\alpha_i)$ 是不是就应该等于：

$\max_{\alpha_i \ge 0} L(w,b,\alpha_i) = \frac{1}{2}||w||^2 - \min_{\alpha_i \ge 0}\{\sum_{i=1}^{m}{\alpha_i(y_i(w\cdot x_i +b )-1)}\}$

因为求最大化一个整体大项，而前面部分与α无关，减法转化为求后面部分的最小值，而前面又有约束条件 $\{ \alpha_i \ge 0 \\ y_i(w\cdot x_i+b) -1 \ge0$ ，则后面部分那一大坨的最小值只能取到0(☺，而后面这一大坨为0也引申出了支持向量的概念，下文再说)，故有：

$\max_{\alpha_i \ge 0} L(w,b,\alpha_i) = \frac{1}{2}||w||^2 - \min_{\alpha_i \ge 0}\{\sum_{i=1}^{m}{\alpha_i(y_i(w\cdot x_i +b )-1)}\} = \frac{1}{2}||w||^2$

故原条件极值问题转化为：

$\min {\frac{1}{2}||w||^2} = \min_{w,b} \max_{\alpha_i \ge 0} L(w,b,\alpha_i)$

此问题不好解，再根据KKT条件，感兴趣的可以去推一下，简单来说就是在特定约束条件下，minmax的问题可以转化为maxmin来求解，这俩称为对偶问题，其对偶问题写为：

$\min_{w,b} \max_{\alpha_i \ge 0} L(w,b,\alpha_i) = \max_{\alpha_i \ge 0} \min_{w,b} L(w,b,\alpha_i)$

则通过求偏导先求min的最值，再求max的最值，即可求解(以偏导为0来求解)：

$\{ \frac{\partial L}{\partial w} = 0 \to w=\sum_{i=1}^m \alpha_i y_i x_i \\ \frac{\partial L}{\partial b} = 0 \to \sum_{i=1}^m \alpha_i y_i = 0$

代入maxmin的式子，有：

$\max_{\alpha_i\ge0} \min_{w,b}L(w,b,\alpha_i)=\max_{\alpha_i\ge0} ({\frac{1}{2}||w||^2}-w\cdot\sum_{i=1}^m \alpha_i y_i x_i-b\cdot\sum_{i=1}^m\alpha_i y_i+\sum_{i=1}^m\alpha_i)$

化简后得：

$\max_{\alpha_i\ge0} \min_{w,b}L(w,b,\alpha_i)=\max_{\alpha_i\ge0} ({\frac{1}{2}||w||^2}-||w||^2 +\sum_{i=1}^m\alpha_i) =\max_{\alpha_i\ge0} (\sum_{i=1}^m\alpha_i-\frac{1}{2}||w||^2)$

最后化为向量内积的形式，至于为啥要化成內积的形式，原因是为了使用kernel，下文会提到：

$\{\max_{\alpha_i\ge0}(\sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i,j=1}^m \alpha_i\alpha_jy_iy_j<x_i,x_j>)\\s.t.\qquad\sum_{i=1}^m\alpha_i y_i=0,\qquad\al_i\ge0$

好了，上式就是最后的求解公式了，求解方式为SMO算法。可见SVM的求解过程是通过拉格朗日方法将约束条件代入，并满足了KKT条件，minmax的问题转化成对偶的maxmin问题，再求解。但在其中，有一些比较interesting的特性，下面来一一说明。

支持向量：

先说一下SVM训练完成后的分类方式：一个新的样例到来，会根据学习到的超平面H，将新样例代入H，即 $f(x)=w\cdot x+b$ ，再判断其正负，来进行分类。而上面求偏导中有 $w=\sum_{i=1}^m \alpha_i y_i x_ib$ ，f(x)转化为向量內积的形式，为 $f(x)=\sum_{i=1}^m\alpha_i y_i \langle x_i, x\rangle + b$ ,看似m维的计算，其实很多α的值都是0。

具体的说就是支持向量的α不为0，其余向量的α都为0，为啥呢？前面的推导也提到了，有 $\max_{\alpha_i \ge 0} L(w,b,\alpha_i) = \frac{1}{2}||w||^2 - \min_{\alpha_i \ge 0}\{\sum_{i=1}^{m}{\alpha_i(y_i(w\cdot x_i +b )-1)}\} = \frac{1}{2}||w||^2$ ，加上两个约束条件，是不是有 $\alpha_i(y_i(w\cdot x_i +b )-1)=0$ ，即两个相乘为0，要不就是 $\alpha_i$ 为0，要不就是 $y_i(w\cdot x_i +b )-1$ 为0，如果后项为0(即该样例落在超平面H1或者H2上，为支持向量)，则其前项可以不为0；而当后项不为0(不是支持向量)，其前项必为0，这就是支持向量的由来。

说了这么多有啥用呢，简单的说就是学习到的模型只用存储这些支持向量就可以了，也提升了计算的速度，也是该算法命名的由来。
kernel：

kernel在这里简单的说一下吧，因为推导实在有点多，具体可以参见支持向量机: Kernel，MIT大牛写的推导。前面我们通篇介绍的SVM都是在线性可分的情况下，而当数据不满足该条件时怎么办呢，就要使用kernel了。

kernel的用处是将原来线性不可分的数据映射到高维空间，使其线性可分。

在介绍支持向量的时候提到了，新样例的分类方式为使用 $f(x)=\sum_{i=1}^m\alpha_i y_i \langle x_i, x\rangle + b$ ，是一个內积的形式，通过映射 $\phi(\cdot)$ 我们可将不可分数据映射到可分空间，则有 $f(x) = \sum_{i=1}^m\alpha_i y_i \langle \phi(x_i), \phi(x)\rangle+b$ ，而映射后维度的扩张导致的计算量是爆炸性的，因为原始维度之间每一个都有组合并且可能扩展到N维。所以机智的人们就想到了使用一些函数来代替映射后的內积，使他们都在同一空间，即完成了先做內积，再做空间映射的工作，从而大大的减少了计算量，并且可以轻松映射到无限维。

例如多项式核 $\kappa(x_1,x_2) = \left(\langle x_1,x_2\rangle+R\right)^d$ 就是先做內积再做映射，分类函数就可以写为： $f(x) = \sum_{i=1}^m\alpha_i y_i \kappa(x_i,x) +b$
outlier:

outlier的作用是控制噪音对SVM的影响，推导还是参见支持向量机：Outliers，简单来说就是将约束条件更改为： $y_i(w\cdot x_i+b)\geq 1-\xi_i$ ，其中 $\xi_i$ 是松弛变量，则目标函数变为： $\min \frac{1}{2}||w||^2+ C\sum_{i=1}^m \xi_i$ ，其中的C用来控制寻找 Margin 最大的超平面和保证数据点偏差量最小之间的权重,推导过程和之前一致。最后的求解公式变为： $\{\max_{\alpha_i\ge0}(\sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i,j=1}^m \alpha_i\alpha_jy_iy_j<x_i,x_j>)\\s.t.\qquad\sum_{i=1}^m\alpha_i y_i=0,\qquad 0\le\alpha_i \le C$

好了，有了以上的补充，就可以得到一个可以处理任何数据，并且能容忍噪音的SVM了。总结一下，SVM求的是两个分类超平面H1和H2之间的最大化距离，而落在这两个超平面上的样例就叫做支持向量，这也是该分类方法命名的由来，并且通过一些数学的补充，最终能处理任何维度的分类问题。

再说说SVM的应用吧，在实验室曾用SVM做过文本分类，分类效果还不错，是要高于一般的分类算法的，但缺点是训练速度较慢，实验室的日子已经过去太久远了。工作中曾经使用过Ranking SVM做搜索排序相关的工作，参见我的另一篇逻辑回归和learning to rank算法以及相关实践，即一个待排序的搜索文本排在另一个之前则值域为1，反之为-1，定义域则为两个搜索文本之间的特征向量相减，以希望发现不同特征之间的差值对排序的影响，属于learning to rank学派，具体参见Support Vector Machine for Ranking，但在实际中使用其代码，在训练数据量很大的情况下(千万级)，算法很难收敛并且速度很慢。

参考:

1: Joachims T. Optimizing search engines using clickthrough data[C]//Proceedings of the eighth ACM SIGKDD international conference on Knowledge discovery and data mining. ACM, 2002: 133-142.
2： Chang C C, Lin C J. LIBSVM: a library for support vector machines[J]. ACM Transactions on Intelligent Systems and Technology (TIST), 2011, 2(3): 27.
3: Burges C J C. A tutorial on support vector machines for pattern recognition[J]. Data mining and knowledge discovery, 1998, 2(2): 121-167.

支持向量：

kernel：

outlier: