逻辑回归对于做算法相关的同学来说应该都比较熟悉,是一个简单易用的线性模型,我第一次使用逻辑回归是上研究生时,有一个paper需要对多种推荐算法的结果进行投票,也就是对每种推荐结果的权重进行学习,其中逻辑回归实验效果还不错(起码是优于单一的协同过滤算法的☺),当时是把逻辑回归的数学推导都过了一遍的,个人认为搞算法的最好是把各种经典算法的数学推导都搞明白,不然在复杂的实际应用中有些算法你implement了,但数据组织、参数、实验的效果解释和调优方向你根本搞不清楚,这就很尴尬了。有点扯远了,回到正题,这一段时间在工作中也用到了逻辑回归,实现的目的简单来说是对搜索建议的结果进行重排序(注意是重排序,也就是说本身有一个人工设定权重的排序公式),其中有很多用户本身、用户输入、搜索建议本身的特征,训练集的正例就是用户点击了某条搜索建议、负例就是没有点击的,数据量较大,每天的正例在2kw级别,负例在10亿+级别。
对于上面的问题,大部分人可能会首先想到逻辑回归,诚然,我们组也尝试了这种方法,但毕竟我们不是广告算法组,而且这种重排序的问题和广告CTR预估还是有差异的(下面会说到具体的差异),所以以前的实验都失败了,失败的主要原因以及解决方案,我事后诸葛亮总结如下:
-
正负样例比例:
以前的算法以及网上的资料对该比例的描述都是比较模糊的,1:2?1:3?1:4?1:5?反正都有人说好,这也是正常的,在不同的展现环境下,上述比例都有可能是最好的。这里需要引入一篇paper[1],这篇可以认为是learning to rank里程碑式的文章,简单来说就是作者认为用户的点击行为(也就是正例)是有偏见的,即对于搜索引擎类似的每条结果从上到下的展示方式来说,用户更倾向于点排在前面的,打个比方,用户点了搜索引擎排在第一条的结果,但这一条在训练集中不一定是正例,排在后面的没点的不一定是负例。
在搜索这种从上到下排序的有偏(Bias)样式中,我更建议用[1]里的训练集组织方式(亲测有效☺),如图举例:

上图是一个搜索引擎返回的排序结果,加粗的是用户点击过的,简单的可以认为3、7是正例,2、4、5、6是负例,即排在后面有正例,前面的才能作为负例。
当然上述的组织方式在使用learning to rank的Pointwise Approach学习的过程中会将大部分权重都学成负(why?因为我们已经有一个人工的权重排序公式了,这样的训练集就是打人工公式的脸,人工排在前面的,都是负例,人工排在后面点击的才是正例),相信大部分搞算法的都碰到过这样的问题。那这部分训练集到底代表了什么样的信息呢?这部分训练集代表了用户在有偏的条件下,还极端的选择了后面的样例,可以肯定后面的样例一定有吸引用户的特征,只不过全部用这类样例来训练模型的话就会过拟了,so我们只需要对原始的排序模型进行采样并合并所有的样例,参见Learning to rank在淘宝的应用,再实施学习算法,基本就能simulate线上的情况,以及学习到的参数你就可解释了,而不是一脸懵逼,能对学习到的参数的变化进行解释非常重要,这是分析调参和分析数据集以及证明你的想法不是瞎BB的基础。 -
特征选取:
“年轻人,不要总想着搞个大新闻。。。”,这句话是前辈老大哥对我们的教导,化简为繁是可以一步一步做的,但化繁为简就比较难了(在大量的特征中做减法真的很难),我们总会听到某搜索巨头逻辑回归特征上亿维,神乎其神,所以总是一上来就想把特征工程做的比较大,但对于一个从0-1的过程来说,不太建议使用太多无谓的特征,首先这些特征不一定有用,然后还会耽误很多宝贵的时间以及需要保证特征的相关代码不出错,最后学习出的参数维度太大,也很难去解释了。数据挖掘在实际中,谁也没有一下子就能保证线上的结果好的,都需要不断的解释修正,所以如果搞出一个巨大无比的模型,而又无法解释模型,就把自己的路堵死了。
所以建议最开始都从少量的人工认为有用的特征开始做,这样算法也快,效果好了模型稳定了还可以继续加特征,话题又回到上面提到的差异:计算广告完成的目的是什么?有很多广告,又有很多用户,我不知道该怎么分发这些广告,而且也没有分发的依据,但我有很多广告和用户的特征,以及用户点击了广告的行为,所以我只要有了以前的日志,就可以学习到用户点广告的规律,这些规律用特征学习到的参数呈现。所以逻辑回归算法是完成一个从无到有的规律探索过程,而且实施了之后一定比目前线上的结果好。而对于搜索引擎来说,一般都会有一个几经锤炼的排序公式了,再用逻辑回归去学习参数,虽然理论上是能提高的,但实际效果提高可能不明显,并且如果再添加一些无用的特征(噪音)来干扰排序,那往往都是适得其反,所以搜索重排序可以看做是一个90到100的过程,那初期就暂时不要添加新的特征了,就用人工排序公式的特征进行学习,那这种算法就是经典的learning to rank(排序学习)了。 -
评估指标:
计算广告CTR预测中的评估指标一般都是AUC,AUC代表的是模型在逻辑回归的sigmod函数后的阈值(0~1)变化的情况下,模型的准确性,关注的是在选定阈值下,哪些是好的结果,哪些是不好的结果,是一个整体的指标,并没有考虑到顺序的比较,而既然用户点击是有偏的,那就说明排序非常重要(其实在搜索日志中,90%左右的用户点击都是第一条结果)。对于搜索等重排序的问题,我们关注的应是一条结果是否应该排在另一条结果前面,所以单纯使用AUC进行评估,可能我AUC很高,但是线上实验很差的情况,故对于搜索中的重排序问题来说,应该使用的是NDCG,其关注的是顺序对结果的影响。
以上三点也是我在项目中所实施的想法,因为评估用的NDCG,在使用线上日志的情况下,初期的模型基本上在线下就能simulate算法的结果,从而为调参和特征的取舍提供了极大的方便(不用线上迭代,就能知道正确与否,基本一下午就能将一个参数敲定),基于这样的一个reasonable的模型,后续的工作也更好拓展,主要集中于特征的增加和数据量的选取了。当然,这样的过程更像是一个learning to rank算法了,逻辑回归和learning to rank其实还是比较相似的,达到的目的都是对特征的权重进行拟合,下面就简单分析一下两个算法的数学以及异同吧~~~
1、logistic regression
逻辑回归就是在线性回归上加入了一个sigmod函数,使值域范围在(0-1)之间,这样更易于根据学习到的值来做分类或者决策,当然sigmod函数也正好可以表示成事件发生的概率(数学的奇妙~~~参见Logistic Regression 之基础知识准备中关于事件发生几率odds的推导):
函数的图像为:
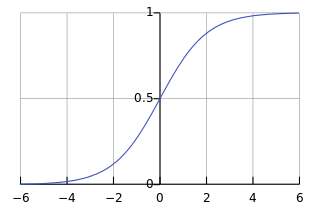
其中s可以看做线性回归得到的值,表示为:
则θ就是学习到的权重向量了,回归算法可以简单的理解成解方程组,比如二元一次方程,我只要有两个等式一般就有解,只不过回归算法求出来的解是权重。还需要说一些概率方面的东西,因为每一个样本的出现是独立的,所以可以认为我的所有训练样例出现的原因都是因为其出现的概率是最大的,假设我们有n个独立的训练样本{(x1, y1) ,(x2, y2),…, (xn, yn)},y={0, 1}。那每一个观察到的样本(xi, yi)出现的概率是:
则所有的训练样例出现的概率表示为,数学中叫做似然函数:
注意其中的θ,上面的公式是关于sigmod函数后的发生概率,故带上θ就是关于所有参数的公式,而θ是权重向量,上面提到了,我所得到的训练样本的出现,是因为其出现的概率大。那对于上面的所有样例出现概率的公式,我只要求其最大值就行了,即求一组θ,使上面公式达到最大值,从而满足我所得到的训练样例,该方法就是机器学习中著名的求解方式MLE(最大似然估计)了。求最值我们都知道一般会用求导来做,但上面的公式求导后无法求解析解,故使用梯度上升法逼近,这一大坨的推导和证明我就不写了,具体可以参见机器学习算法与Python实践之(七)逻辑回归(Logistic Regression)和从最大似然到EM算法浅解,写的已经很清晰了。
最后得到的θ向量就是各个参数的权重了,预测的时候做一个乘法并累加就可以了。逻辑回归的优势是算法比较简单,训练也比较快且得到的模型你能解释(解释每一个权重,非常重要),所以工业界大量的使用,劣势是一个线性模型,对于高维的情况效果不太好,不过也可以人为创造一些高维特征。
2、learning to rank
learning to rank貌似会比较小众一些,这几年炒的也不温不火,工业界搞的比较好的是MSRA,不过貌似涉及到搜索排序的,都会用这个来搞一搞,算法主要用于对排序公式的参数进行拟合优化(当人工调参很难进行的时候,因为人工一般只能关注一个参数的变化带来的影响),LTR有三种思路,分别是Pointwise Approach、Pairwise Approach、Listwise Approach,具体的请参见Learning to rank学习基础,算法也比较多,但最终都还是对特征的权重进行拟合。
说一下RankSVM,因为这个是我在实际工作中使用了的,比较有发言权吧,并且很多公司做learning to rank也是使用的RankSVM。那还是要说回paper[1],该论文的两大法宝第一个就是上面说过的训练样例组织方式,去掉了大部分Bias数据,第二个就是RankSVM了,论文也证明了使用该算法的效果好(☺),SVM的数学可以参见我的另一篇推导。
RankSVM的思想简单说就是通过用户的点击or非点击样例形成两两的对(所以其属于Pairwise Approach),正例->负例就是新正例,负例->正例就是新负例,那么就可以通过分类问题来表示排序问题,具体的请看[1],下面用图说明一下:
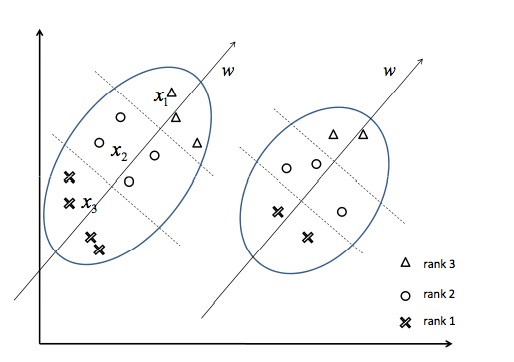
点x3是得分最高的,x2、x1次之,这是一个典型的排序问题,在实际中用户点或者不点可以看成是得分高或者不高(0、1表示),转化为pair对之后如下图:
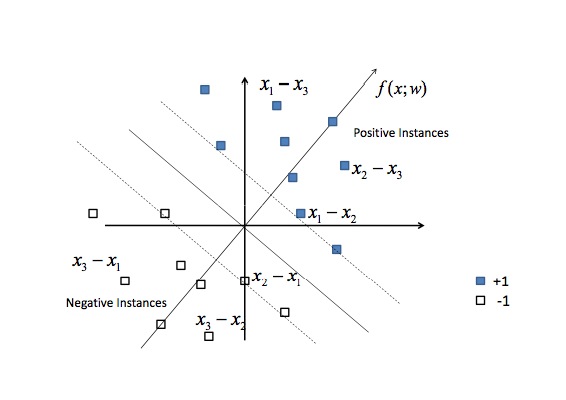
即通过x1-x2、x1-x3、x3-x1等等的特征向量相减,将问题转化成了一个考虑了两两排序差异原因(由相减带来,很机智呀)的分类问题。
论文作者还刁刁的给出了算法的开源实现,参见Support Vector Machine for Ranking。
剩下的就很好搞了,按代码的要求组织好数据,扔进去调一调参数,看看效果就ok,不过我在使用linux版本的源码中,在训练集在亿级的时候,算法很难收敛并且速度非常慢,所以如果数据量太大最好需要做一些交叉验证或者采样的工作。训练完毕后其会同逻辑回归一样产生一个参数模型,预测也是做一个乘法就可以了。
参考:
-
1: Joachims T. Optimizing search engines using clickthrough data[C]//Proceedings of the eighth ACM SIGKDD international conference on Knowledge discovery and data mining. ACM, 2002: 133-142.
-
2: Li P, Wu Q, Burges C J. Mcrank: Learning to rank using multiple classification and gradient boosting[C]//Advances in neural information processing systems. 2007: 897-904.
-
3: Li, Hang. “Learning to Rank for Information Retrieval and Natural Language Processing.”
-
4: Liu T Y. Learning to rank for information retrieval[J]. Foundations and Trends in Information Retrieval, 2009, 3(3): 225-331.