Deep Learning in One Page | 睡不醒的景耕

按叙事的手法来说，在工作中使用过一次Word2Vector(为了参加公司的黑马大赛☺)，因为需要在两天之内完成后端相关算法，所以调用了Mikolov的相关代码，然后为了完成PPT(☺)也大致看了一下算法理论。但是还是感觉不求甚解，所以在经历了种种数学公式的折磨之后，有了这篇文章，本文主要参考了Andrew在Stanford的Deep Learning教程，诸君可以仔细看看，其网站上还有中文的翻译，非常靠谱，算是自学DL最好的中文教材了。次要参考了一些牛人的见解和思路，也加深了对于算法的理解，相关链接我会放在文章后面的reference中。

毕竟DL是一门历久弥香的学派，所以涉及的知识点和数学推论非常多，非常多(神经网络激活函数的背景还得需要看看生物)。。。我写此篇文章的目的是为了理解其背景以及数学的物理意义，还有目前热门DL相关算法的思想。这样不仅仅是只知道这样用代码，还知道为什么这么用，以及未来还可以怎么用，达到触类旁通的效果。所以本文会比较长，主要先对Deep Learning的相关历史沿革、知识点进行梳理，然后再对其热门的算法进行详细讲解。至于为什么给这篇文章取了”Deep Learning in One Page”，是因为最近看了《The Universe in Your Hand》，觉得在一篇教程里把Deep Learning讲清楚也是极好的。

最后会有一个我自己的Word2Vector实践，思路也比较简单，在我司的某热门产品中，可以得到用户输入的词，将用户所有的词经过Word2Vector转成词向量后，便可以得到很多和用户输入词相关的词，然后将这些词中用户没见过的推荐给用户，从而达到推荐词引导用户点击带流量的目的，从效果上来看还是不错的(起码对于我司黑马大赛的演示应该够了，比如用户曾输入过周杰伦，给他返回方文山☺)。

一、先来点有意思的

引用了Deep Learning 实战之 word2vec的一张《大牛图》：

大牛们

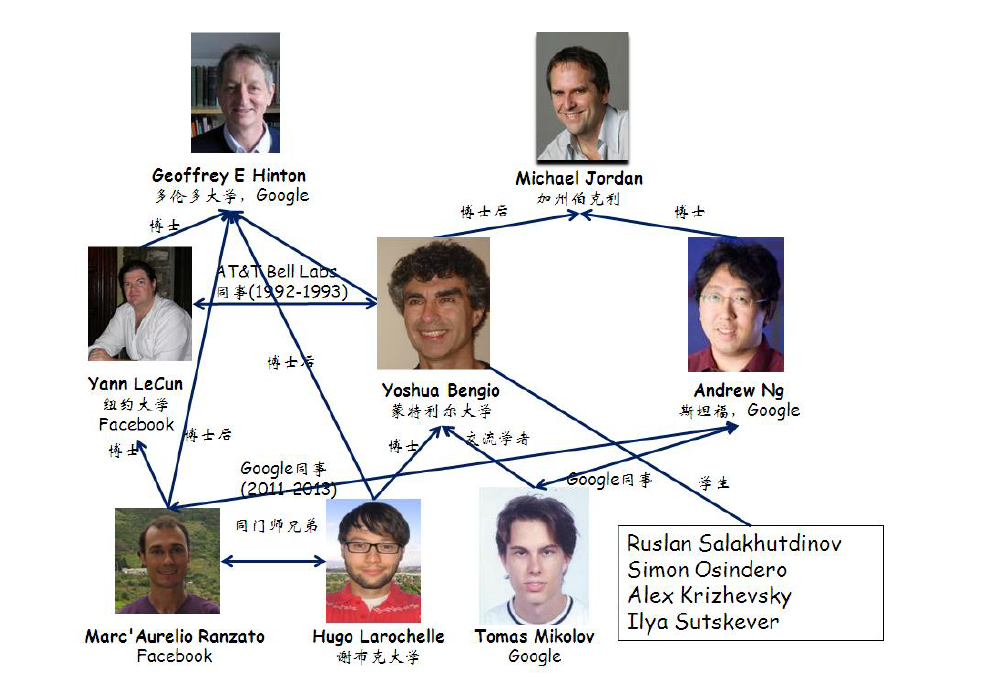
树的根节点分别是Hinton老大爷和Jordan(当然不是打篮球那个Jordan)，Hinton可以说是在神经网络方面耕耘了几十年，在NN最不被人看好的那些年依然没有放弃。Jordan也是NN老司机以及扫地僧的角色，有一种哥不在江湖，但江湖总有哥的传说的既视感，可以看看和伯克利的Michael Jordan教授一起工作是什么感觉？再往下是LeCun、Bengio、Andrew(年轻的Andrew老师挺胖的☺)，分别是推动卷积神经网络的大神、神经概率语言模型的大神、早期LDA到如今将DL发扬光大的大神。最后的还有Ranzato、Larochelle、Mikolov。

近几十年NN发展中的milestone差不多是由以上的大牛们提出来的，当然这是一个英雄创造历史还是历史创造英雄的问题，不过大牛提出的original的建模思想确实是创造性的，不是我等follow一下思想再改改就能发文章的套路。话说回来，科学探索是一个人类认识真理的过程，目前来说，不管是理论上还是实践中，深度神经网络确实是一个既有理论支持又有实践效果的模型，可能在将来会有更好的模型超越它，我也期待能见到那一天。那深度神经网络到底完成了一个什么功能呢？它的强大之处在哪里呢？我认为是完成了(或者说模拟了)生物对于事物的认识过程，换句话说，神经网络达到的目标是：自动对事物的特征进行有效抽象。那如何抽象以及为啥要抽象呢？这是一个人类认识各种事物理解各种事物的过程，下面要开门放生物学了(☺)。

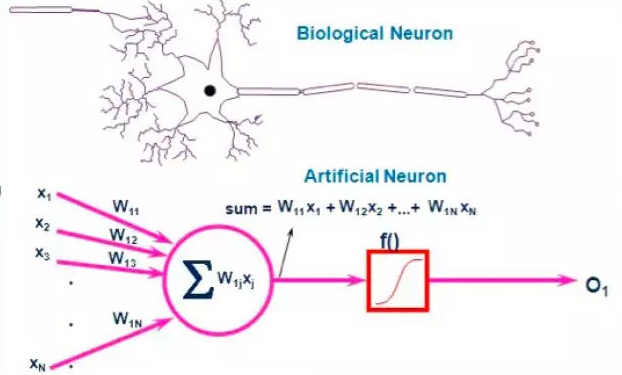
ANN模型

我就直接上图说了，因为毕竟是CS出身，生物上的东西也没有太多研究。上图是一个生物上的神经网络和人工神经网络的对比，简单的可以理解为左边部分的神经元完成了对输入信号的处理，并抽象该信号送给中间部分进行传输，右边部分是输出或者说将该抽象信号传递到一个新的神经元进行下一步处理，人工神经网络是完成了对生物神经网络的一种数学建模。

再上一个例子，引用自Deep Learning（深度学习）学习笔记整理系列之（一）：

1958 年，DavidHubel 和Torsten Wiesel 在 JohnHopkins University，研究瞳孔区域与大脑皮层神经元的对应关系。他们在猫的后脑头骨上，开了一个3毫米的小洞，向洞里插入电极，测量神经元的活跃程度。

然后，他们在小猫的眼前，展现各种形状、各种亮度的物体。并且，在展现每一件物体时，还改变物体放置的位置和角度。他们期望通过这个办法，让小猫瞳孔感受不同类型、不同强弱的刺激。

之所以做这个试验，目的是去证明一个猜测。位于后脑皮层的不同视觉神经元，与瞳孔所受刺激之间，存在某种对应关系。一旦瞳孔受到某一种刺激，后脑皮层的某一部分神经元就会活跃。经历了很多天反复的枯燥的试验，同时牺牲了若干只可怜的小猫，David Hubel 和Torsten Wiesel 发现了一种被称为“方向选择性细胞（Orientation Selective Cell）”的神经元细胞。当瞳孔发现了眼前的物体的边缘，而且这个边缘指向某个方向时，这种神经元细胞就会活跃。

这个发现激发了人们对于神经系统的进一步思考。神经-中枢-大脑的工作过程，或许是一个不断迭代、不断抽象的过程。

这里的关键词有两个，一个是抽象，一个是迭代。从原始信号，做低级抽象，逐渐向高级抽象迭代。人类的逻辑思维，经常使用高度抽象的概念。

可见在生物学上，起码在视觉方面，生物认识和抽象一个事物的过程确实是经过了神经网络从而得到其意义(或许现在的科学还无法完全解释和证明，但如果有一天人们彻底理解了自己如何理解事物的过程，AI的时代才会真正来临吧)。上面的例子还有一些其他的启发意义，比如抽象的信号只需要激活少数神经元，比如视觉问题的处理可以初步抽象为方向或者边缘，即可以用少量的带有边缘的图片组合成其他图片，这又和下面的一个例子不谋而合，这次是Andrew老师的分享。

稀疏编码

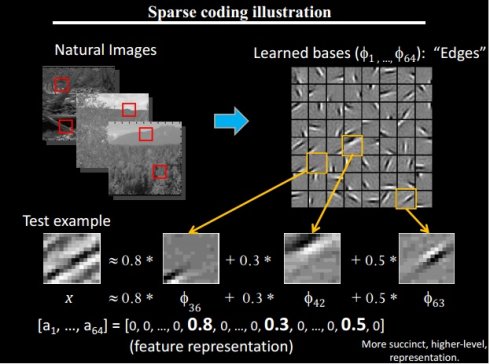
上图右上侧是提取出来的带有边缘的图片，也叫做图片的正交基，共64个，而所有自然图片中的一小块都可以用这64个正交基组合而成，所以这64个图片可以作为对所有图片建模的神经网络的第一层，也就是特征抽象的第一层，再由这些第一层的特征组合成第二层的特征，在下面的图中，从下往上第二层明显可以看出是对第三层图片实体的一部分进行抽象，而这些第二层抽象可以只由第一层特征组合生成。而以第二层为基础特征的时候，则可以明确的识别第三层图片中所表达的实体(意义)。那这三层就可以看作是一个简单的人工神经网络的例子了，即人工神经网络模型模拟了自然界生物如何识别事物的过程，并将其数学化。也许正因为其模拟了生物的认知过程，所以效果超过了目前所有的数学模型，记得有一句话是“人类一直在探索自身认识世界的过程。”

简单神经网络建模

再进行一个举一反三的过程，既然图像可以抽象出基础特征进行神经网络建模，那声音是不是也可以呢？答案是肯定的。那自然语言是不是也可以呢？答案也是肯定的，所以DL一下子火了起来，大家纷纷在自己的领域套用DL。

二、基础知识

来一点严谨的数学吧，下面的每个知识点都是依据Stanford的Deep Learning教程，有些我会将其原因和物理意义补充一下，有些我会举一些例子，有些也会加入一些个人的理解，最后也会进行一个梳理，让各位能够明白Deep Learning的整体流程以及各个知识点在算法中所发挥的作用。本节知识点较多，个人知识也有限，如有错误还望各位指正。

1、神经网络：

神经元

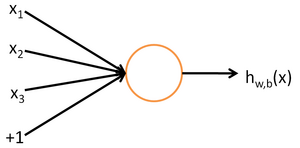
上图是构成神经网络的最小单元：神经元，其完成的工作即是对输入信号进行抽象并输出。以上图的图示来说，其拥有3个输入信号 $x_1,x_2,x_3$ 以及一个偏置项(也叫截距) $+1$ ，则其输入与输出关系表示为：

$h_{w,b}(x) = f(W^Tx) = f(\sum_{i=1}^{3}{W_ix_i + b})$

其中函数 $f$ 称为“激活函数”。激活函数可以有很多，但依据Andrew老师的教程，使用的是sigmod函数：

$f(z) = sigmod(z) = \frac {1}{1 + \exp(-z)}$

则该神经元完成的功能其实是一个逻辑回归进行分类的过程，逻辑回归相关可以参考我的另一篇文章。当然，激活函数常用的还有双曲正切函数(tanh)，表示为：

$f(z) = tanh(z) = \frac {e^z - e^{-z}}{e^z + e^{-z}}$

其与sigmod的区别为sigmod值域为[0,1]，tanh值域为[-1,1]。

那由多个神经元组成的网络模型即是神经网络了，以下公式及推论搬运自Andrew老师的课程，如下图所示：

神经网络

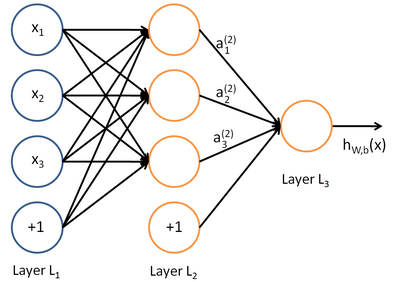
我们用 ${n}_l$ 来表示网络的层数，本例中 $n_l=3$ ，我们将第 $l$ 层记为 $L_l$ ，于是 $L_1$ 是输入层，输出层是 $L_{n_l}$ 。本例神经网络有参数：

$(W,b) = (W^{(1)}, b^{(1)}, W^{(2)}, b^{(2)})$

其中 $W^{(l)}_{ij}$ (下面的式子中用到)是第 $l$ 层第 $j$ 单元与第 $l + 1$ 层第 $i$ 单元之间的联接参数(其实就是连接线上的权重，注意标号顺序)， $b^{(l)}_i$ 是第 $l + 1$ 层第 $i$ 单元的偏置项。因此在本例中， $W^{(1)} \in \Re^{3\times 3}$ ， $W^{(2)} \in \Re^{1\times 3}$ 。

注意，没有其他单元连向偏置单元(即偏置单元没有输入)，因为它们总是输出 $1$ 。同时，我们用 $s_l$ 表示第 $l$ 层的节点数(偏置单元不计在内)。

我们用 $a^{(l)}_i$ 表示第 $l$ 层第 $i$ 单元的激活值(activition)。当 $l=1$ 时， $a^{(1)}_i = x_i$ ，也就是第 $i$ 个输入值(输入值的第 $i$ 个特征)。对于给定参数集合 $W,b$ ，我们的神经网络就可以按照函数 $h_{W,b}(x)$ 来计算输出结果。本例神经网络的计算步骤如下：

$a_1^{(2)} = f(W_{11}^{(1)}x_1 + W_{12}^{(1)} x_2 + W_{13}^{(1)} x_3 + b_1^{(1)})$

$a_2^{(2)} = f(W_{21}^{(1)}x_1 + W_{22}^{(1)} x_2 + W_{23}^{(1)} x_3 + b_2^{(1)})$

$a_3^{(2)} = f(W_{31}^{(1)}x_1 + W_{32}^{(1)} x_2 + W_{33}^{(1)} x_3 + b_3^{(1)})$

$h_{W,b}(x) = a_1^{(3)} = f(W_{11}^{(2)}a_1^{(2)} + W_{12}^{(2)} a_2^{(2)} + W_{13}^{(2)} a_3^{(2)} + b_1^{(2)})$

我们用 $z^{(l)}_i$ 表示第 $l$ 层第 $i$ 单元输入加权和(包括偏置单元)，比如 $z_i^{(2)} = \sum_{j=1}^n W^{(1)}_{ij} x_j + b^{(1)}_i$ ，则 $a^{(l)}_i = f(z^{(l)}_i)$ 。

这样我们就可以得到一种更简洁的表示法。这里我们将激活函数 $f$ 扩展为用向量(分量的形式)来表示，即：

$f([z_1, z_2, z_3]) = [f(z_1), f(z_2), f(z_3)]$

那么，上面的等式可以更简洁地表示为：

$z^{(2)} = W^{(1)} x + b^{(1)}$

$a^{(2)} = f(z^{(2)})$

$z^{(3)} = W^{(2)} a^{(2)} + b^{(2)}$

$h_{W,b}(x) = a^{(3)} = f(z^{(3)})$

上面的整个神经网络建模过程名叫前向传播，即从输入层开始，层层传递直到输出层，传递是一个递归的过程，即给定第 $l$ 层的激活值 $a^{(l)}$ 后，第 $l + 1$ 层的激活值 $a^{(l + 1)}$ 就可以按照下面步骤计算得到：

$z^{(l + 1)} = W^{(l)} a^{(l)} + b^{(l)}$

$a^{(l + 1)} = f(z^{(l + 1)})$

以上就是神经网络建模的全过程，以及前向传播算法，上面的公式不少，其实理解起来也比较简单，这么多公式呢主要是为了下一节反向传播算法做准备(☺)。

2、反向传播算法：

BP这一章本来是想按照Andrew老师的教程展开的，但发现其讲义实在是太精简，公式都不带推导的。。。中文的译者给加上了部分推导，但理解起来还是比较费劲，主要难点在代价函数关于每一层参数 $W_{i,j}$ 的偏导的求解过程，以及其中残差(error term)的定义，中间涉及的一些知识点链式法则和Delta规则文中都没有提及，废话不多说，容我从头梳理一遍。

先上代价函数：

$J(W,b; x,y) = \frac{1}{2} \left\| h_{W,b}(x) - y \right\|^2$

符号意义同上一节，其中 $y$ 代表样例的标签，即某样例 $(x,y)$ 是对应神经网络的输入和标签，而 $h_{W,b}(x)$ 是输入经过神经网络后的输出，则代价函数 $J$ 求的是样例输入经过神经网络后的输出与样例标签的差异。

那按照MLE的套路，只要在训练样例下最小化代价函数 $J$ 就可以了，即不断的调整代价函数中的参数 $W_{i,j}$ 和 $b_i$ ，使代价函数最小。

调整的方式是使用这两个参数的梯度 $\frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x, y)$ 和 $\frac{\partial}{\partial b_{i}^{(l)}} J(W,b; x, y)$ 来迭代，直到满足代价函数的可接受最小值(阈值)或者达到最大迭代次数，梯度的求解是一个求偏导的过程(求偏导的物理意义是函数关于变量变化而变化的快慢)。如果这一段你有点懵逼，建议你先看看MLE和GD，好了，剩下的就是两个参数在神经网络中求梯度的方法了，该方法就是反向传播算法。

先求 $W_{i,j}$ 的梯度，Andrew的讲义中 $\frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x, y)$ 是使用两项相乘的方式，其中一项为残差。公式是准确的，并且先求解了残差，这就是一个先有鸡还是先有蛋的问题了，我个人认为残差确实有助于理解算法，也使求解更加美观，但残差应该是求解 $\frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x, y)$ 的产物，其中使用了链式法则，故为两项相乘的方式，下面直接上 $\frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x, y)$ 的推导过程：

$\frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x, y) = \frac {\partial J}{\partial f(z^{l + 1})}\frac {\partial f(z^{l + 1})}{\partial z^{l + 1}}\frac {\partial z^{l + 1}}{\partial W_{ij}^{(l)}}$

上式使用了复合函数求导的链式法则，相关符号遵循上一节的神经网络，现对后面三项分别求解：

$\frac {\partial f(z^{l + 1})}{\partial z^{l + 1}} = f'(z^{(l + 1)}) = f(z^{l + 1}) (1-f(z^{l + 1}))$

其中 $f$ 是激活函数，本公式使用的sigmod，在Andrew的讲义中，没有按sigmod展开，只计算到等式前两项。

$\frac {\partial z^{l + 1}}{\partial W_{ij}^{(l)}} = \frac {\partial (\sum_{j=1}^nW_{ij}^{(l)}a_j^{(l)} + b_i^{(l)})}{\partial W_{ij}^{(l)}} = a_j^{(l)$ ，这项没啥可说的，套用了上一节的公式，并且加入了下标，其中 $b_i^{(l)}$ 与所求偏导不相关，所以去掉了。

$\frac {\partial J}{\partial f(z^{l + 1})}$ 这一项要分两种情况进行讨论：

第一种是 $z^{l + 1}$ 是网络最后一层，也就是输出层，即 $f(z^{l + 1}) = a^{(nl)}$

则 $\frac {\partial J}{\partial f(z^{l + 1})} = \frac {\partial (\frac{1}{2} |y-a^{(nl)}|^2)}{\partial a^{(nl)}} = -({y-a^{(nl)})$

第二种是 $z^{l + 1}$ 是网络的中间层，即隐藏层，则也可利用链式法则

$\frac {\partial J}{\partial f(z^{l + 1})} = \frac {\partial J}{\partial z^{nl}} \frac {\partial z^{nl}}{\partial f(z^{nl-1})}\....\frac {\partial z^{l + 2}}{\partial f(z^{l + 1})}$

从后往前求得，这也是该算法叫反向传播的原因，而其中的中间项之一可以解为：

$\frac {\partial z^{l + 2}}{\partial f(z^{l + 1})} = \frac {\partial (W^{(l + 1)}f(z^{l + 1}) + b^{(l + 1)})}{\partial f(z^{l + 1})} = W^{(l + 1)$

这里就引入一下残差 $\delta^{(l)}_i$ 了，上一个链式法则的式子如果真要展开也是能展开的(只是比较难看)，然而大牛们为了优雅(☺)引入了单层的能量损失来使公式更漂亮，不过确实对理解算法有帮助，并且残差也有其物理意义。残差是：

$\frac{\partial}{\partial z^{l}_i}J(W,b;x,y) = \delta^{(l)}_i = ( \sum_{j=1}^{s_{l + 1}} W^{(l)}_{ji} \delta^{(l + 1)}_j ) f'(z^{(l)}_i)$

物理意义即代价函数关于关于某一层 $l$ 中激活函数的输入 $z^l$ 的偏导，所以隐藏层 $l + 1$ 的偏导可写为：

$\frac {\partial J}{\partial f(z^{l + 1})} = \sum_{j=1}^{s_{l + 2}} W^{(l + 1)}_{ji} \delta^{(l + 2)}_j$

将上面推导过的三项乘起来，并引入残差化简：

$\frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x, y) = \delta^{(l + 1)} (a^{(l)})^T$

公式确实很漂亮。顺便一提该公式中残差是按照这层的输入 $(a^{(l)})$ 加权到这层的权重 $W_{ij}^{(l)}$ 中，即在网络训练的过程中，残差会按输入的比例调整参数的大小，这也是一种反向传播的过程。

剩下的就很好解了，使用梯度下降迭代求解，我就不多说了，再提一个代价函数关于截距 $b$ 的偏导，为：

$\frac{\partial}{\partial b_{i}^{(l)}} J(W,b; x, y) = \delta_i^{(l + 1)}$ ，比较简单，请各位自行推导。

以上就是BP的推导了，简单的说，反向传播得到了整体代价函数关于神经网络中每一层参数 $W_{ij}^{(l)}$ 和 $b_{i}^{(l)}$ 的梯度，从而可以用梯度下降法对其进行MLE求解。最后Delta规则提一下，可以理解其为单层网络中的梯度推导过程。

3、稀疏自编码：

先说一下自动编码器(AutoEncoder)，具体的内容可以参见。在上一节讲到的BP算法，其实是一个很老的算法了，在上世纪80年代就已经很成熟，但其并没有带来神经网络的成功，原因是通过BP计算的网络中每一层的参数不好解释，即不能知道网络中某一层所抽象出来的意义是什么。

那么自动编码器可以做到这一点，简单的自动编码器规定网络的输入经过隐藏层之后，所得到的输出依然等于输入，看上去这个定义挺二的，比如使用一个恒等式就完成了，但当对自动编码进行一些约束之后，比如隐藏层节点数远小于输入层节点数(这样会迫使隐藏层学习关于输入信息的更加正交的表达，比如通过10个隐藏层节点的组合，表达出输入层100个节点的信息)，即可以得到对输入信号的正交基(信号主要方向)的抽象，如果你熟悉PCA，这一块应该很好理解，也可以看看我的另一篇SVD、LSA(LSI)、PCA、PLSA、LDA的数学以及一个SVD的实践。

然后就是稀疏自编码器(SparseAutoEncoder),稀疏是指隐藏层中每个节点的神经元的激活值都趋近于0，为啥要加一个稀疏性呢，各位可以想象上一章提到的生物学中猫的视觉实验，在猫的眼前呈现的不同方向的不同物体，只激活了猫大脑中的部分神经元，即生物中神经网络的激活是有稀疏特性的。则稀疏自编码器的代价函数为：

$J(W, h) = ||Wh - y||_2^2 + \lambda ||h||_1$

其中 $h$ 是隐藏层的激活值， $W$ 是该层中关于激活值的权重， $y$ 是输出层， $\lambda$ 是惩罚项的系数，其中右侧的惩罚项常常使用一阶范数(L1)或者二阶范数(L2)，本例中使用的是一阶范数。则求解上述公式得到的是最小化网络对输入信号的抽象错误值与隐藏层神经元惩罚项的和，其实是在学习对输入信号的最优表达。

最后可以看看Andrew老师的一个例子，其使用稀疏自编码器在图像数据上训练了100个隐藏神经元的结果：

稀疏自编码训练结果

和第一章的例子有点像，不过可以明显的看出其得到了图像中边缘和方向的抽象，也就是组成图像的一个比较优秀的基特征，并且还和生物上的实验惊人的相似，并且得到该抽象的过程是无监督的，这样就更适合大规模计算了。

总结一下这个小节，稀疏自编码通过无监督的方式得到了对于输入数据的另一个更加正交的表达(或者说是抽象)，这样隐藏层层层递推，就可以在有限的层数下得到对输入数据的高级抽象表达(如果上面那个图算低级的话)，这样就是得到了数据中有用的特征，并且注意是无监督得到的。

4、Softmax回归：

简单的说，softmax就是逻辑回归分类在N维上的推广，或者说logistic是softmax的一个特例，即softmax可以对输入数据进行分类，分类输出是该输入分到每一类的概率的向量。想想在实际应用中，logistic的二分类应用范围确实不多，所以在deep learning算法中就大量使用了softmax，比如MNIST的手写数字识别，至于为啥使用softmax做分类而不用其他分类算法，我个人的理解是：简单，好调试(☺)。这一节比较简单，如果对逻辑回归不熟悉可以看看我的一篇逻辑回归和learning-to-rank算法以及相关实践，下面给出数学推导及求解，部分使用了Andrew课程的内容：

数据集为： $\{ (x^{(1)}, y^{(1)}),...,(x^{(m)}, y^{(m)}) \}$ ，其中 $y^{(i)} \in \{1, 2, \ldots, k\}$ ， $k$ 是分类数目。

对于给定的测试输入 $x$ ，我们想用假设函数针对每一个类别j估算出概率值 $p(y=j | x)$ 。也就是说，我们想估计 $x$ 的每一种分类结果出现的概率。因此，我们的假设函数将要输出一个 $k$ 维的向量(向量元素的和为1)来表示这 $k$ 个估计的概率值。具体地说，我们的假设函数 $h_{\theta}(x)$ 形式如下：

$h_\th(x^{(i)}) =\left[p(y^{(i)}=1|x^{(i)};\th)\\p(y^{(i)}=2|x^{(i)};\th)\\\vdots\\p(y^{(i)}=k|x^{(i)};\th)\right]=\frac{1}{\sum_{j=1}^{k}e^{\th_j^Tx^{(i)}}}$ $\left[e^{ \theta_1^T x^{(i)} } \\ e^{ \theta_2^T x^{(i)} } \\ \vdots \\ e^{ \theta_k^T x^{(i)} } \\ \right]$

其中 $\theta_1, \theta_2, \ldots, \theta_k \in \Re^{n 1}$ 是模型的参数。请注意 $\frac{1}{ \sum_{j=1}^{k}{e^{ \theta_j^T x^{(i)} }} }$ 这一项对概率分布进行归一化，使得所有概率之和为1。

注意上面公式的假设函数是向量的形式，在有些参考资料中，将其中一项拎出来了，即该输入分到其中一类的概率，写为：

$p(y^{(i)} = j | x^{(i)} ; \theta) = \frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{ \theta_l^T x^{(i)}}}$

表达的是一个意思，但是从拎出来的公式中，可以得到一个冗余特性以及softmax退化到logistic的推导，如下：

Softmax 回归有一个不寻常的特点：它有一个“冗余”的参数集。为了便于阐述这一特点，假设我们从参数向量 $\theta_j$ 中减去了向量 $\psi$ ，这时，每一个 $\theta_j$ 都变成了 $\theta_j - \psi(\textstyle j=1, \ldots, k)$ 。此时假设函数变成了以下的式子：

$p(y^{(i)} = j | x^{(i)} ; \theta) = \frac{e^{(\theta_j-\psi)^T x^{(i)}}}{\sum_{l=1}^k e^{ (\theta_l-\psi)^T x^{(i)}}}$ $= \frac{e^{\theta_j^T x^{(i)}} e^{-\psi^Tx^{(i)}}}{\sum_{l=1}^k e^{\theta_l^T x^{(i)}} e^{-\psi^Tx^{(i)}}}$ $= \frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{ \theta_l^T x^{(i)}}}$

可见在一般代价函数下，其解是不唯一的，所以类似logistic的正则化，唯一解的代价函数会加入一个关于参数 $\theta$ 的正则项，其不仅惩罚了过拟的参数值，并且使得解唯一。

然后是从sofxmax退化到logistic的推导，当 $k = 2$ 时，softmax回归的假设函数为：

$h_\theta(x) = \frac{1}{ e^{\theta_1^Tx} + e^{ \theta_2^T x^{(i)} } } \left[e^{ \theta_1^T x } \\ e^{ \theta_2^T x }\right]$

利用softmax回归参数冗余的特点，我们令 $\psi = \theta_1$ ，并且从两个参数向量中都减去向量 $\theta_1$ ，得到：

$h(x) =\frac{1}{ e^{\vec{0}^Tx} + e^{ (\theta_2-\theta_1)^T x^{(i)} } } \left[ e^{ \vec{0}^T x } \\ e^{ (\theta_2-\theta_1)^T x } \right]$

$= \left[ \frac{1}{ 1 + e^{ (\theta_2-\theta_1)^T x^{(i)} } } \\ \frac{e^{ (\theta_2-\theta_1)^T x }}{ 1 + e^{ (\theta_2-\theta_1)^T x^{(i)} } } \right]$

$= \left[ \frac{1}{ 1 + e^{ (\theta_2-\theta_1)^T x^{(i)} } } \\ 1 - \frac{1}{ 1 + e^{ (\theta_2-\theta_1)^T x^{(i)} } } \\ \right]$

因此，用 $\theta'$ 来表示 $\theta_2-\theta_1$ ，我们就会发现softmax回归器预测其中一个类别的概率为 $\frac{1}{ 1 + e^{ (\theta')^T x^{(i)} } }$ ，另一个类别概率的为 $1 - \frac{1}{ 1 + e^{ (\theta')^T x^{(i)} } }$ ，这与 logistic回归的sigmod函数写出的分类结果是一致的。

最后softmax的代价函数写为：

$J(\theta) = - \frac{1}{m} \left[ \sum_{i=1}^{m} \sum_{j=1}^{k} 1\left\{y^{(i)} = j\right\} \log \frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{ \theta_l^T x^{(i)} }}\right]$

其中 $1\{\cdot\}$ 是示性函数，其取值规则为： $1 \{ true \} = 1$

加入正则化项(L2)的代价函数为：

$J(\th)=-\frac{1}{m}\left[\sum_{i=1}^{m}\sum_{j=1}^{k} 1\{y^{(i)}=j\}\log\frac{e^{\th_j^Tx^{(i)}}}{\sum_{l=1}^ke^{\th_l^Tx^{(i)}}}\right] + \frac{\lam}{2}\sum_{i=1}^k\sum_{j=0}^n\th_{ij}^2$

梯度下降求解上面的代价函数，偏导为：

$\nabla_{\theta_j} J(\theta) = - \frac{1}{m} \sum_{i=1}^{m}{ \left[ x^{(i)} ( 1\{ y^{(i)} = j\} - p(y^{(i)} = j | x^{(i)}; \theta) ) \right] } + \lambda \theta_j$

至此，softmax就介绍完了，总结一下，讲了假设函数、代价函数、代价函数的梯度求解、冗余特性、利用冗余特性使softmax退化到logistic。最后提一下softmax(包括logistic)这么解得到的是什么，可能有些人比较懵逼，从代价函数来看，得到的是在训练集下学习到的参数 $\th$ ，并且该 $\th$ 是使在训练集情况下分类错误(代价函数)最小的，所以我们认为该 $\th$ 是模型训练的最优参数，这也是MLE算法的数学假设，再提一下MLE的提出是费希尔，他的故事可以参考统计学杂史《女士品茶》，非常有意思。

5、逐层贪婪 && 微调：

上面讲了这么多基础知识，终于到了融会贯通的时候了，回顾一下本章，先说了神经网络，然后是神经网络的梯度解法反向传播，然后是稀疏自编码，稀疏编码迫使网络抽象出数据的主要特征，所以一般用稀疏编码来构建神经网络的中间层，中间层逐层抽象输入的特征，最后是softmax，softmax(或者logistic)一般用于神经网络的最后一层，即在最后一层上会对抽象的输入特征进行一个分类的工作。网络的训练则通过有限的标注数据，对网络进行反向传播训练所有层的参数，这些参数的初始值使用随机初始化，如图所示：

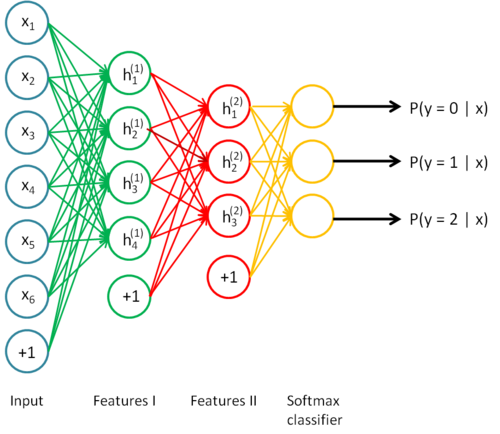
神经网络组成结构

看起来是不是很完美，然而并没有，其实上图的模型几十年前就有了，但为啥Deep Learning这几年才大放异彩呢？原因就是在多层网络的结构下，随机初始化后反向传播训练出来的参数往往会陷入局部最优解(因为代价函数非凸)以及深层网络中梯度值在网络最初的几层会很小导致很难训练。这些问题又是如何解决的呢，那就是本小节的内容了，可以说是最近DL取得成功的计算基础之一。

逐层贪婪说起来也挺简单的，就是去掉了网络中所有参数的随机初始化，而使用逐层贪婪得到的参数作为初始化参数。具体来说是从输入层开始，先构建一层稀疏自编码作为隐藏层，然后在这个两层网络上直接进行训练，因为稀疏自编码是无监督的，所以可以学习到关于两层的最优抽象表达，然后在这两层的基础上继续构建下一层，再训练，以此类推，逐层都追求最优的抽象表达，最后还是加上一个分类器作为输出层，这样一个逐层取最优参数的过程故而名为逐层贪婪。为什么要这么做呢，其实就是为了解决局部最优解的问题，逐层贪婪得到的初始参数经过反向传播后往往能得到神经网络更优的解。

微调可以看做是反向传播的过程，在逐层贪婪下，反向传播每次更新参数都是一次微调，并且微调后的参数可以大幅提升神经网络的正确性。

好了总结一下，一个基础的可用的深度神经网络数学模型就出来了，包括了建模、求解、优化，其他的模型都是基于上面的知识点做了一些计算或者特定场景建模的优化，包括了卷积神经网络(CNN)、递归神经网络(RNN)、Word2Vector等，下面章节一一介绍。

三、经典模型

1、卷积神经网络：

卷积神经网络是DL的一项重要应用算法，尤其在图像处理方面，其成功之处在于对大图像的局部感受野和权值共享使需训练的神经网络参数大大减少，并且使特征具有平移，旋转不变性。下面首先来谈一下卷积的物理意义。

1.1、卷积的物理意义：

卷积的物理意义大部分参考资料中都没有提及，也不知道是什么原因，我觉得有必要说一下，理解了卷积才能理解CNN的数学假设。引用知乎上的回答怎样通俗易懂地解释卷积？，卷积的物理意义是：“一个函数（如：单位响应）在另一个函数（如：输入信号）上的加权叠加。”，可表示为：

$\int_{ - \infty }^{ \infty } {f(r)g(t-r)dr}$

上式中 $f(r)$ 是输入信号函数， $g(t-r)$ 是单位响应函数，积分是推广到了连续的情况下。即对于所有的(负无穷到无穷)输入信号单位响应，都对输入信号进行了相乘并叠加，其中单位响应可以理解为权重。那卷积的意义是如何应用到神经网络上的呢？这就是局部感受野和卷积神经网络的数学假设了。

1.2、局部感受野：

直接上图说明：

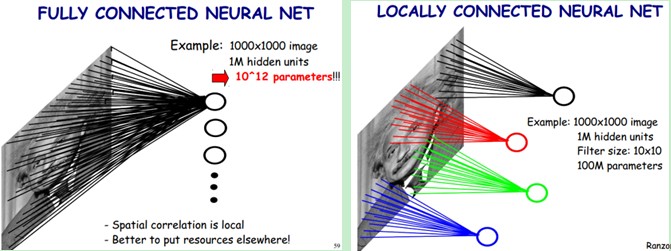
局部感受野

左图是一个全联通网络，图像输入有1000*1000像素，假如你需要学习100万个特征(即隐藏层神经元数量)，由于是全联通网络，则该层需要训练的权重参数 $W$ 数量级为10的12次方(1000*1000*100万)，已经非常大了，那如何改进这种结构呢？答案就是部分联通网络，顾名思义部分联通就是隐藏层神经元只连接上一层网络的部分输入，如右图例子还是需要学习100万个特征的神经元，但这些神经元只连接图像的某个10*10像素，那是不是需要训练的参数数量级下降为10的8次方了(1000*1000*10*10)。那这10*10个像素起一个高大上的名字就是局部感受野。

当然这也是受启发于生物学里面的视觉系统结构。视觉皮层的神经元就是局部接受信息的（即这些神经元只响应某些特定区域的刺激）。那局部感受野又是怎么和卷积扯上关系的呢？先谈谈图像特征的复用性，卷积神经网络的数学假设也是基于此，从第一章的视觉例子中大家也应该看出来了，第一个隐藏层得到的特征输入可以得到第二个隐藏层的带有明显轮廓的特征，即一张图像的特征可以复用到另一张图像，推广一下就是图像的一部分的统计特征与其他部分是一样的。

则可以将局部感受得到的隐藏层特征神经元作为卷积中的输入信号 $f(r)$ ，按局部感受野的像素大小作为最小单元，分解遍历整个图像(即公式积分的过程)，将遍历到的每个最小单元的像素值作为单位响应 $g(t-r)$ ，最后相乘，就可以得到整幅图像关于局部感受野特征的卷积。

再通俗一点就是通过局部感受野得到一个特征神经元(比如用稀疏自编码得到)，其权重参数为 $W$ 已知，这个 $W$ 即是 $f(r)$ (不考虑偏置项)，图像中剩下的所有像素都使用这个特征神经元作为输入信号去探测响应，得到卷积。即一个局部感受野的特征神经元的权重参数 $W$ 是作用在整个图像上的，就是下一小节要说的权值共享。

1.3、权值共享：

上面已经把权值共享的原理说的差不多了，下面使用Andrew的例子来说明一个特征神经元取得卷积特征的过程：

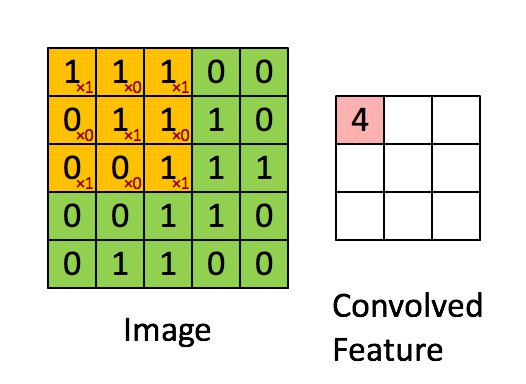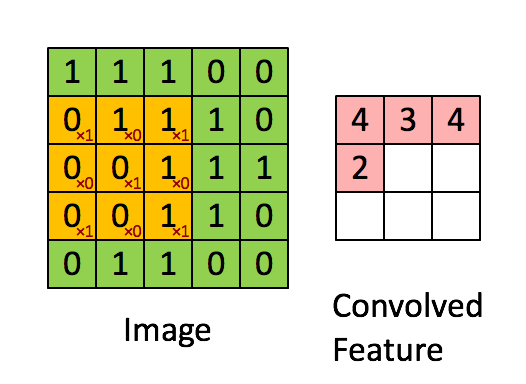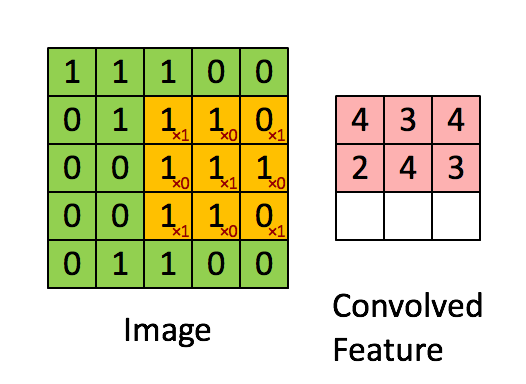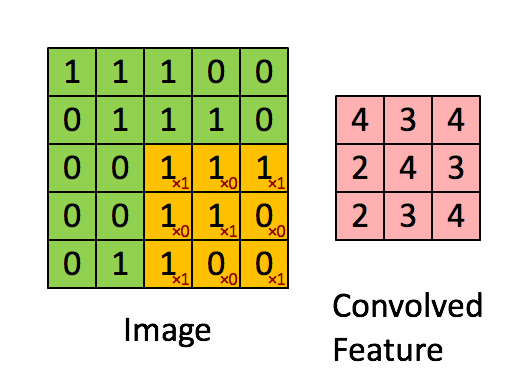
CNN卷积过程

假设你已经从一个 5x5 的图像中学习到了它的一个 3x3 的样本所具有的特征。假设这是由有 1 个隐含单元的自编码完成的。为了得到卷积特征，需要对 5x5 的图像的每个 3x3 的小块图像区域都进行卷积运算。也就是说，抽取 3x3 的小块区域，并且从起始坐标开始依次标记为（1，1），（1，2），…，一直到（3，3），然后对抽取的区域逐个运行训练过的稀疏自编码来得到特征的激活值。在这个例子里，显然可以得到 1 个集合，每个集合含有 (5-3+1)x(5-3+1) 个卷积特征。

通用表达为：假设给定了 $r \times c$ 的大尺寸图像，将其定义为 $x_{large}$ 。首先通过从大尺寸图像中抽取的 $a \times b$ 的小尺寸图像样本 $x_{small}$ 训练稀疏自编码，计算 $f = \sig(W^{(1)}x_{small} + b^{(1)})$ （σ 是一个 sigmoid 型函数）得到了 k 个特征，其中 $W^{(1)}$ 和 $b^{(1)}$ 是可视层单元和隐含单元之间的权重和偏差值。

对于每一个 $a \times b$ 大小的小图像 $x_s$ ，计算出对应的值 $f_s = \sig(W^{(1)}x_s + b^{(1)})$ ，对这些 $f_{convolved}$ 值做卷积，就可以得到 $k \times (r - a + 1) \times (c - b + 1)$ 个卷积后的特征的矩阵。

再回到上面的例子，如图：

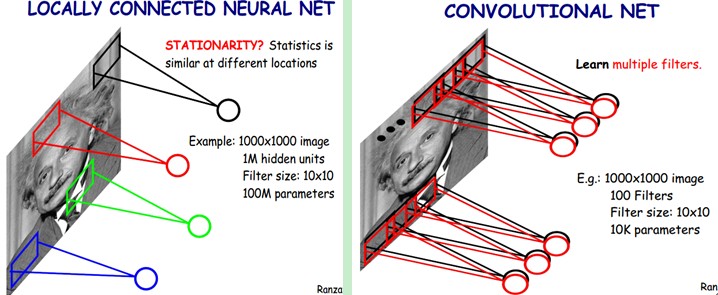
多核卷积神经网络

左图还是10的8次方个参数，那如果我去掉隐藏层的取得方式而使用上面得到的卷积特征作为神经网络的下一层呢？即通过局部感受野得到的特征神经元对整体图像的卷积矩阵作为输入图像的下一层网络(简单说一下为什么这样可行，首先特征神经元已经是局部的一个特征抽象了，再用该特征对整体图像做卷积，得到的是整体图像关于某个特征的抽象，也就是输入图像的另一种表达)，这样的训练参数将进一步减少，相当于减少了隐藏层的神经元数量，如右图，使用了100个局部感受野得到的特征神经元，则需要训练的参数为10的4次方(100个局部感受野得到的特征神经元*每个神经元局部感受范围10*10)。

1.4、池化：

池化简单的说还是为了解决训练特征维度过大的问题，Andrew的讲义很清楚，我就直接引用了：

在通过卷积获得了特征(features)之后，下一步我们希望利用这些特征去做分类。理论上讲，人们可以用所有提取得到的特征去训练分类器，例如 softmax 分类器，但这样做面临计算量的挑战。例如：对于一个 96X96 像素的图像，假设我们已经学习得到了400个定义在8X8输入上的特征，每一个特征和图像卷积都会得到一个(96 − 8 + 1)*(96 − 8 + 1) = 7921 维的卷积特征，由于有 400 个特征，所以每个样例(example)都会得到一个 892 * 400 = 3,168,400 维的卷积特征向量。学习一个拥有超过 3 百万特征输入的分类器十分不便，并且容易出现过拟合(over-fitting)。

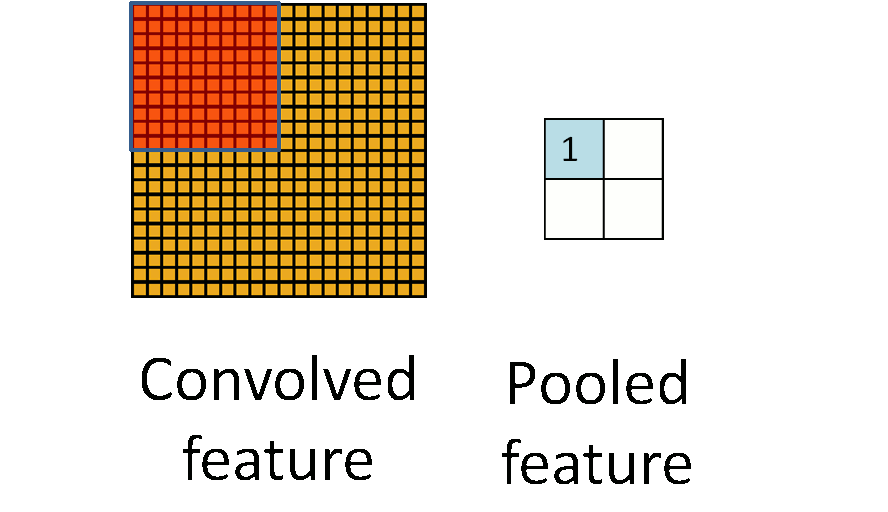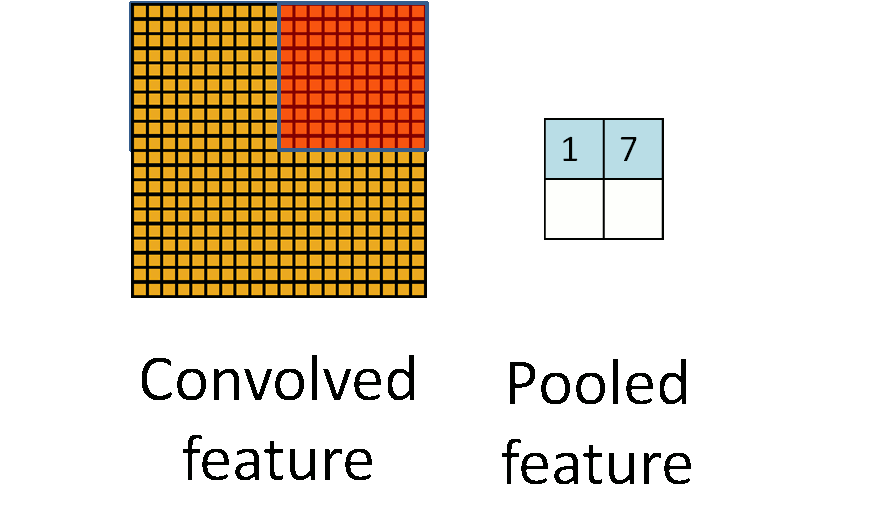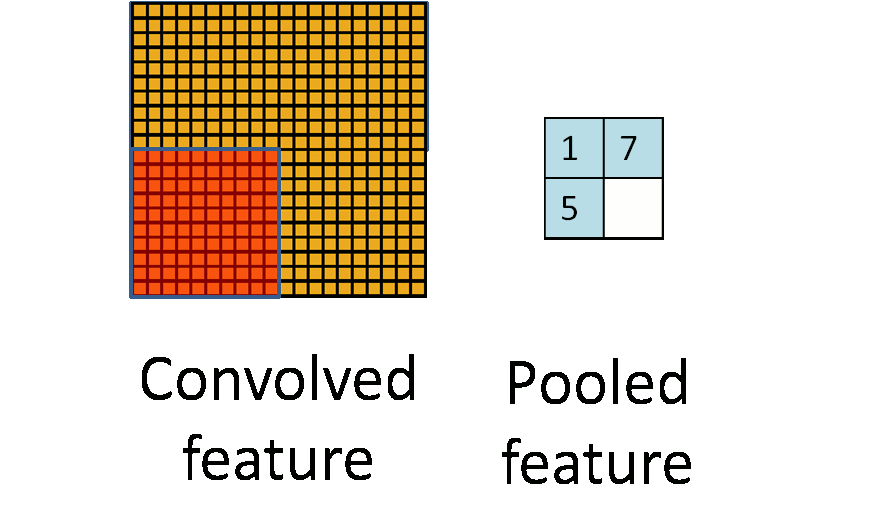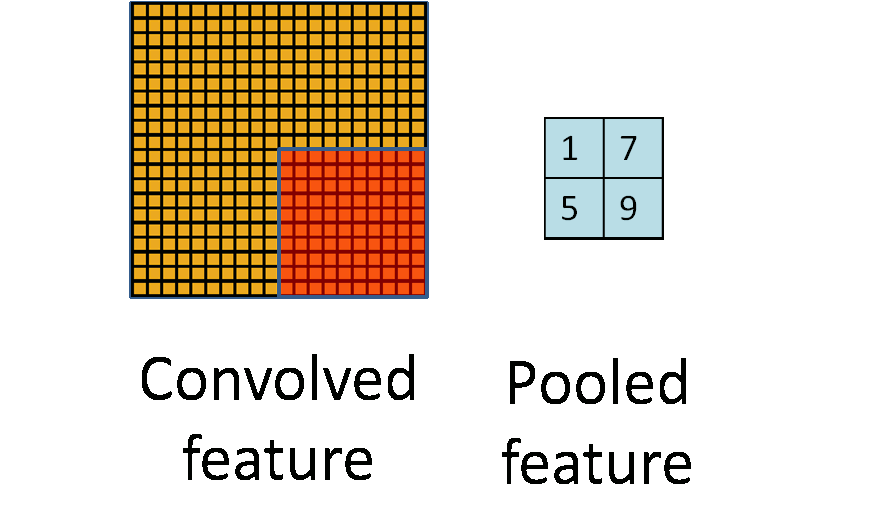
为了解决这个问题，首先回忆一下，我们之所以决定使用卷积后的特征是因为图像具有一种“静态性”的属性，这也就意味着在一个图像区域有用的特征极有可能在另一个区域同样适用。因此，为了描述大的图像，一个很自然的想法就是对不同位置的特征进行聚合统计，例如，人们可以计算图像一个区域上的某个特定特征的平均值(或最大值)。这些概要统计特征不仅具有低得多的维度(相比使用所有提取得到的特征)，同时还会改善结果(不容易过拟合)。这种聚合的操作就叫做池化(pooling)，有时也称为平均池化或者最大池化(取决于计算池化的方法)。

下图显示池化如何应用于一个图像的四块不重合区域。

1.5、LeNet-5的例子：

上面说了很多知识点，这一小节主要目的是将其串起来，并给出一个具体例子来加深理解。用一句话来说，卷积神经网络使用局部感受野抽取一部分特征，则减少了隐藏节点关于输入节点的连接数量，并对全部输入做卷积，就可以得到整体输入关于局部特征的卷积矩阵(对整体输入做了局部感受特征的抽象)，再用少量的局部感受野得到的卷积矩阵替代隐藏层节点(相当于减少了隐藏节点的数量)，再在后面进行池化操作，这样层层递推，在神经网络的高层就可以得到关于输入的低维特征表达，并且需要训练的参数将大大减少。

LeNet-5是一个经典的CNN例子，其用于图像中的手写数字识别，如图所示：

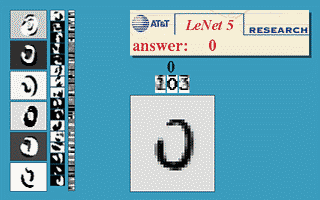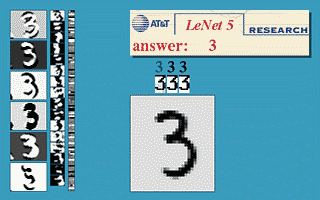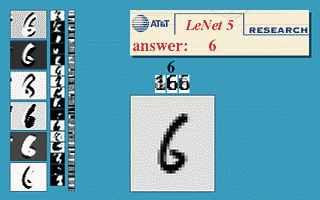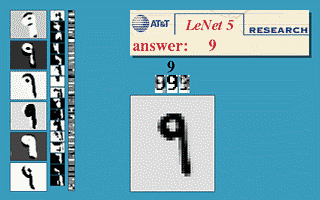
LeNet5

其经典结构为：

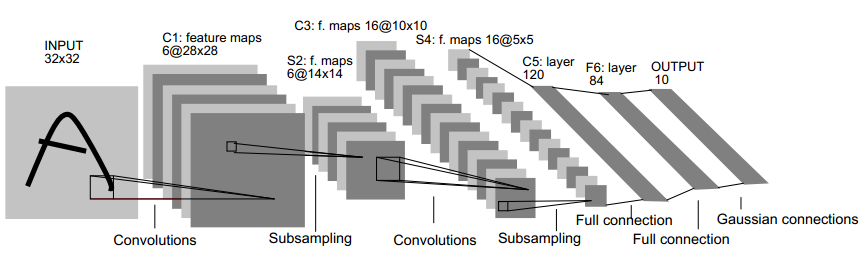
LeNet5结构

输入为32*32的图像，C1是第一个卷积层，其使用6个5*5的局部感受野得到的特征神经元对输入求卷积矩阵并作为C1层的节点，故C1层的大小为6*(32-5+1)*(32-5+1) = 6*28*28。S2层是一个池化层，S2对C1中的2*2大小进行池化，故S2层的大小为6*14*14，后面的层类似，值得一提的是，S2到C3使用的是16个6*5*5的局部感受野对S2求卷积矩阵，网络最后的几层使用了全联通网络。

2、递归神经网络：

递归神经网络的产生其实是基于一些实际问题，比如翻译、语音识别等，完成这些任务常常需要结合历史信息才能准确推断当前最合适的结果。即对神经网络的输入引入了时间维度，当然我们可以收集所有时间维度的输入信息并将其整合成一个大的神经网络输入进行训练，但这样需训练的参数会非常多，并且有些特定的场景下当前时间的状态是跟上一个时间的状态相关的，比如一首歌曲某个时间的声音是跟上一个时间状态声音的震动和当前时间状态发出的声音相叠加的。

简单的说，递归神经网络使用上一个时间状态的隐层输出和当前时间状态的输入作为输入，得到当前状态隐层的输出。

RNN是目前DL能够大行其道的基石，现在主流DL的构建都需要用到RNN，一些在图像、声音上的DL也是用CNN做抽取，中间层全是RNN。这一点也可以从RNN的应用来证明，RNN在机器翻译、同声传译、QA问答、图像实体识别、图像标注、视频标注等方面都有惊人的表现，当然还有一些更厉害的比如学写莎士比亚的散文、学写latex数学证明、学写C++代码等等。总之一句话就是非常NB，非常好玩。

2.1、一个简单的RNN模型：

下面直接上图说明RNN的前向传播过程：

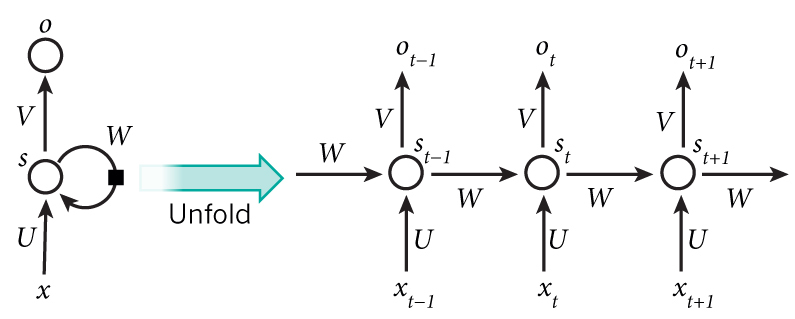
RNN分解

在某时刻 $x_t$ ，隐层神经元 $S_t$ 的输入为：

$a_h^t = \sum_i{w_{ih}x_i^t} + \sum_{h'}{w_{h'h}b_{h'}^{t-1}}$

输出为：

$b_h^t = f(a_h^t)$

其中， $w_{ih}$ 为输入层到隐藏层需学习的权重参数， $x_i^t$ 为输入层某个神经元的输入值， $w_{h'h}$ 为上一个时刻隐藏层的输出到当前时刻隐藏层需学习的权重参数， $b_{h'}^{t-1}$ 为上一个时刻隐藏层某个神经元的输出， $f$ 是非线性激活函数，通常使用tanh。

隐藏层传递到输出层后，若使用softmax进行分类，则输出层的输入为：

$a_k^t = \sum_h{w_{hk}b_h^t}$

输出为：

$y_k^t = \frac {e^{a_k^t}}{\sum_j{e^{a_j^t}}}$

其中， $w_{hk}$ 为隐藏层到输出层需学习的权重参数， $y_k^t$ 是softmax分类。

再来说一下RNN的反向传播过程，其使用BPTT(back propagation through time)算法，其实就是残差项需要加入下一时刻隐藏层的反馈：

$\delta_h^t = f'(a_h^t)(\sum_k \delta_k^tw_{hk} + \sum_{h'} \delta_{h'}^{t + 1}w_{hh'})$

其中输出层的残差为：

$\delta_k^t = y_k^t - z_k^t$

则三个需要学习的权重参数的偏导为：

$\frac {\partial O}{\partial w_{ih}} =\delta_h^tx_i^t$

$\frac {\partial O}{\partial w_{hk}} =\delta_k^tb_h^t$

$\frac {\partial O}{\partial w_{h'h}} =\delta_k^tb_{h'}^t$

再利用梯度下降等方法就可以求解RNN了。可以看到，每个时刻RNN隐层神经元利用上一个时刻隐层神经元的输出和本时刻输入层神经元的输入，得到本时刻隐层神经元的输出。

2.2、梯度爆炸和梯度消失：

从第二章对反向传播算法的介绍以及上一个小节的推导，可知每个时刻残差的传递都需要乘上函数 $f$ 的导数。在时刻序列的数量很大的情况下，当 $f' <1$ 时，残差是不是会呈指数级减小，直至无限趋近于0？代表梯度下降训练过程中神经网络的参数变化会越来越小，直至没有了训练的意义(达不到调优和RNN的初衷)，这个问题就称作梯度消失。再换一个情况，当 $f' >1$ 时，残差会呈指数级增大，无限趋近于无穷，代表梯度下降训练过程中神经网络的参数变化会越来越大，同样会影响训练，这个问题称作梯度爆炸。相关的经典论文请参考Bengio的On the difficulty of training recurrent neural networks。

这两个问题在普通神经网络的结构下也存在，当网络层数很多(深层网络)的情况下，残差从最高的输出层传递到底层时也会出现同样的问题。

2.3、LSTM：

为了解决梯度爆炸和梯度消失问题，提高网络和训练的有效性，大牛们提出了LSTM(long short term memory)，论文可以参考S Hochreiter, J Schmidhuber的LSTM开山之作，LSTM在理论和应用中都达到了不错的效果，现阶段使用的RNN一般都是以LSTM为代表。

如果用一句话来描述LSTM的优势的话，就是使用接近常数1的 $f$ 的导数来进行梯度的反向传播，从而解决了梯度爆炸和梯度消失问题，即神经网络能够记忆很久以前的训练数据作用于本次参数学习。

下面直接上LSTM和普通RNN的对比图：

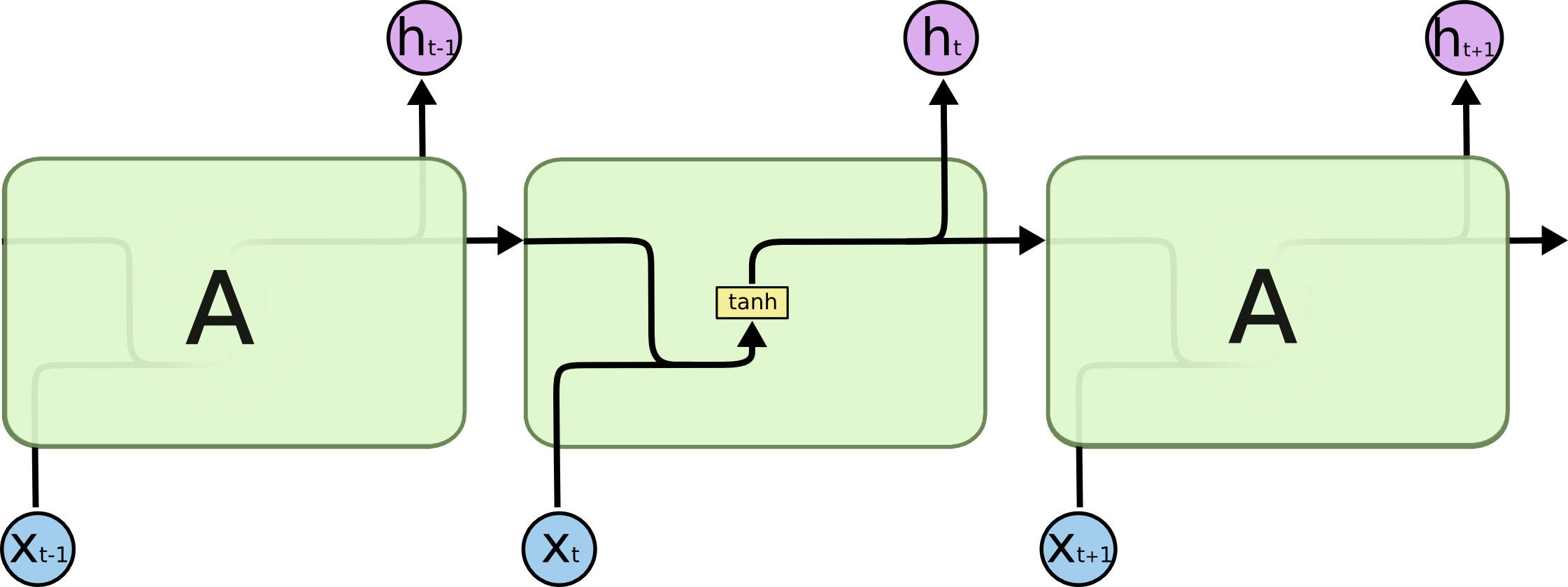
普通RNN

普通RNN结构

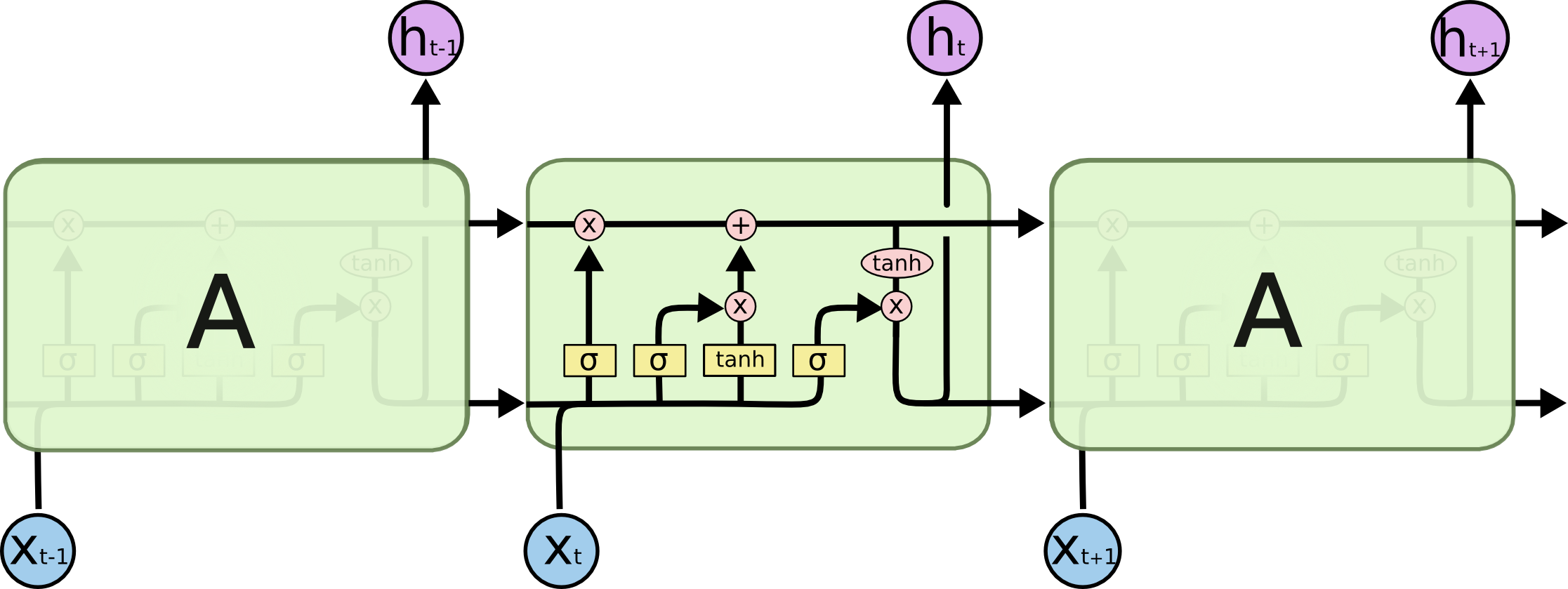
LSTM结构

LSTM结构

从上面的对比图可以看出LSTM多了一些 $\sig$ 函数(下图中标为黄色的区域)，算法将它们称作门，其实就是一个sigmod函数，输入是本时刻输入和上一个时刻隐藏层输出，依然有一个待训练的权重参数 $W$ ，从左到右三个门分别称作遗忘门、输入门、输出门。图中粉色区域代表数值操作，比如粉色X代表输入的两项相乘。tanh就代表以tanh作为激活函数，下面讲一下LSTM的前向传播过程。

遗忘门

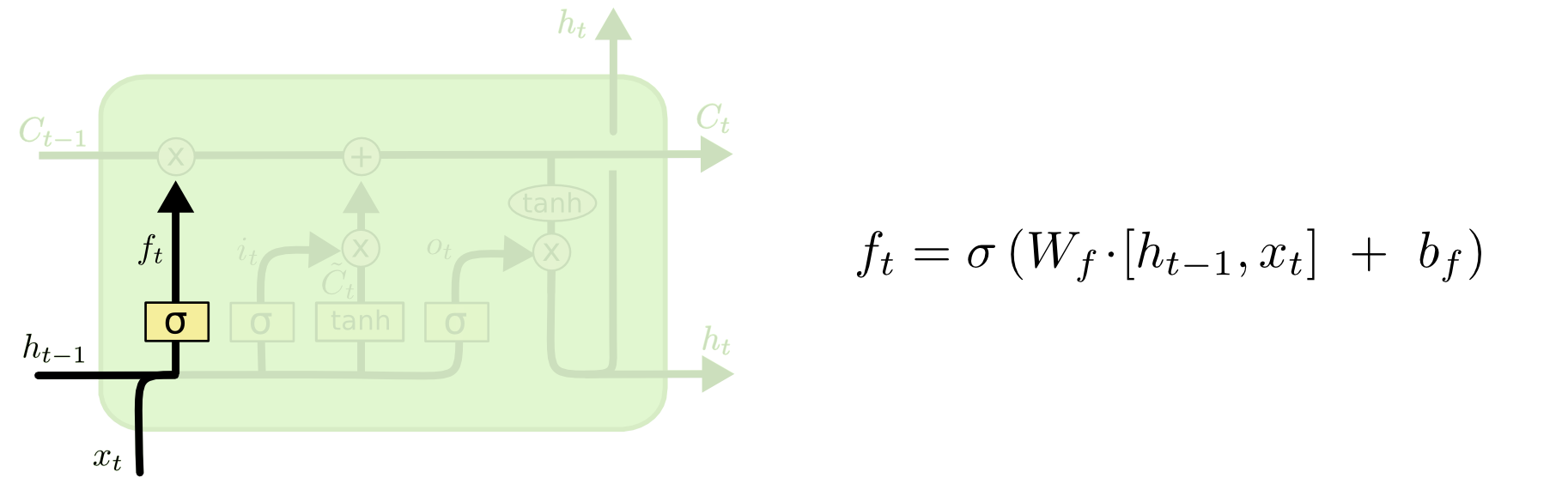
上图是遗忘门，遗忘门用来控制本时刻隐藏层的计算是否遗忘上一个时刻记忆单元的状态值(即是否记忆以前的训练结果)，其中 $\sig$ 是一个sigmod函数，值域为[0-1]， $W_f$ 表示遗忘门需要训练的权重参数， $h_{t-1}, x_t$ 分别表示上一个时刻隐藏层输出和本时刻神经网络的输入， $b_f$ 表示偏置项。 $f_t$ 为1代表不遗忘上个时刻记忆单元的状态值，为0则反之。

输入门

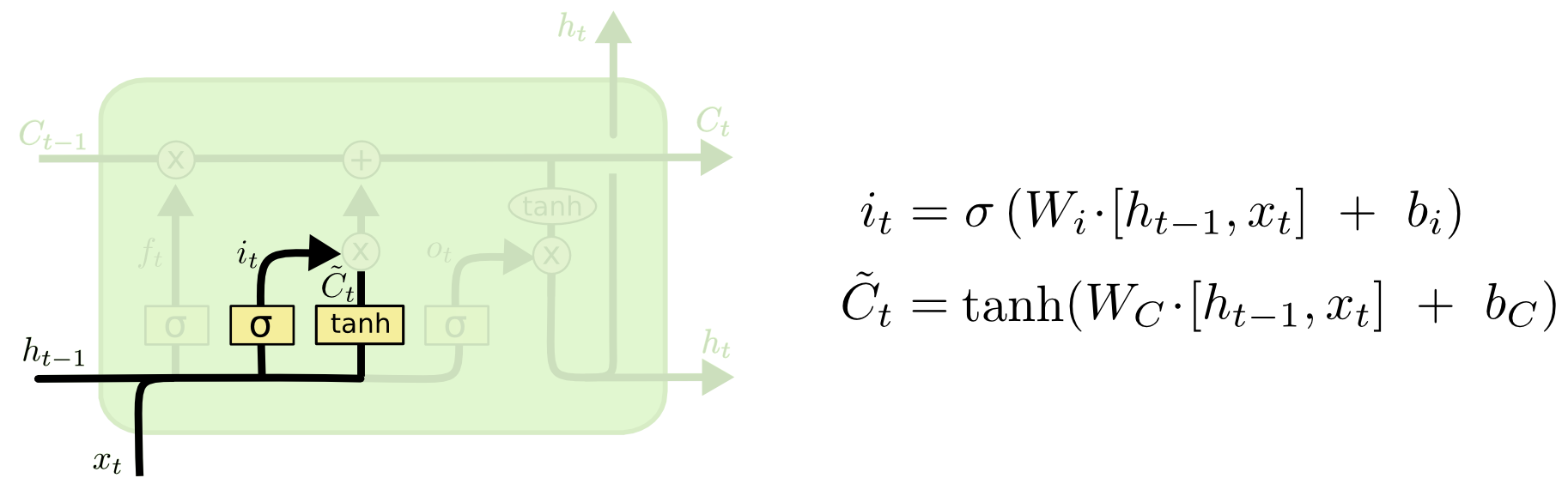
上图左边的 $\sig$ 是输入门，输入门用来控制本时刻隐藏层的计算是否使用本时刻神经网络的输入，其中 $\sig$ 依然是sigmod函数， $W_i$ 表示输入门需要训练的权重参数， $h_{t-1}, x_t$ 的表示同遗忘门一样， $b_I$ 是偏置项， $i_t$ 为1代表使用本时刻神经网络的输入，为0反之。上图右边的tanh函数是本时刻输入层的激活函数，其中 $W_C$ 表示激活函数需要训练的权重参数， $b_C$ 是偏置项。 $\tilde{C}_t$ 是本时刻待加权的神经网络输入。

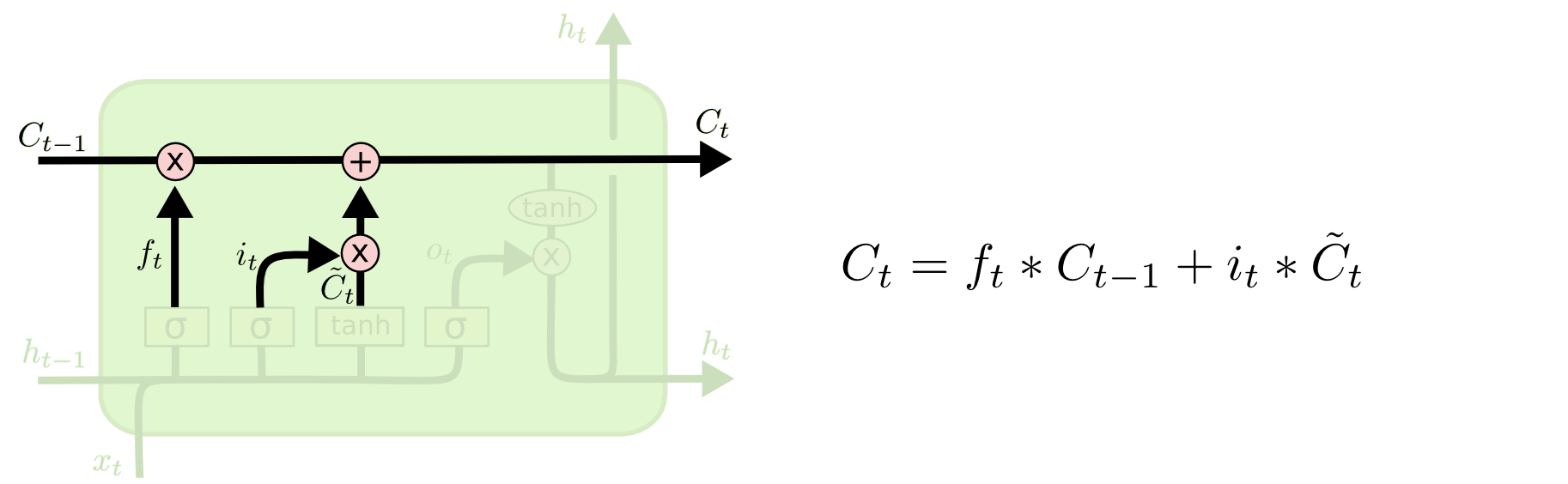
memory cell更新

上图所示即是LSTM隐藏层神经元更新策略，可以看到遗忘门 $f_t$ 控制上一个时刻记忆单元的状态值 $C_{t-1}$ ，输入门 $i_t$ 控制本时刻神经网络的输入 $\tilde{C}_t$ ，本时刻记忆单元的状态值 $C_t$ 由刚刚提到的几项相加得来，如上图右边所示公式。

输出门

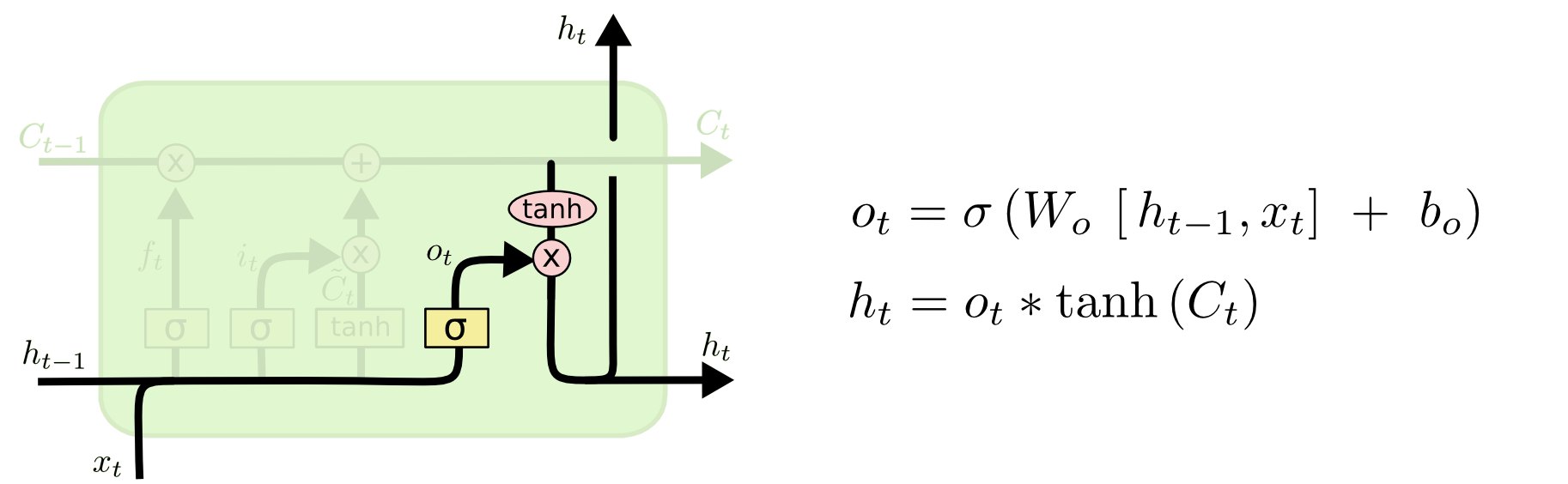
上图左边的 $\sig$ 是输出门，输出门用来控制本时刻隐藏层输出的计算是否使用本时刻隐藏层神经元的状态值，其中 $\sig$ 也是sigmod函数， $W_o$ 表示输出门需要训练的权重参数， $b_o$ 是偏置项， $o_t$ 为1代表使用本时刻隐藏层按记忆单元的状态值得到的输出，为0反之。同样，tanh函数是隐藏层输出的激活函数， $C_t$ 是本时刻记忆单元的状态值， $h_t$ 是本时刻隐藏层的输出。

至此LSTM的前向传播过程就完成了，反向传播过程我就不推了。。。因为实在是太多，各位感兴趣可以去参考LSTM网络（Long Short-Term Memory ），或者LSTM创始论文，细节会比较多一些，思想还是在反向传播过程中，残差(梯度)在记忆单元中的传递会乘上一个接近于1的导数值，故可以用很长时刻前的训练结果作用于本次训练，并且规避了梯度爆炸和梯度消失问题。

3、Word2Vec：

这一节本来和上面的两节关系并不是很大，因为上两节是经典的可复用数学模型，而这一节是独立的一个模型，但因为Word2Vec的名气实在是太大了，所以确实值得好好研究一下，并且其效果也是非常不错的。Word2Vec本质是一个基于神经网络的语言模型，词向量只是其训练出的副产品，但这个词向量却非常实用，因为词向量给出了每个词低维空间的表示，所以对比TFIDF等来说计算量更小，并且能够表达近义词之间的相关性。

3.1、神经概率语言模型：

论文请参见Bengio的《A Neural Probabilistic Language Model》，神经网络语言模型的开山之作，开启和推动了一系列神经网络用于自然语言处理的研究工作。

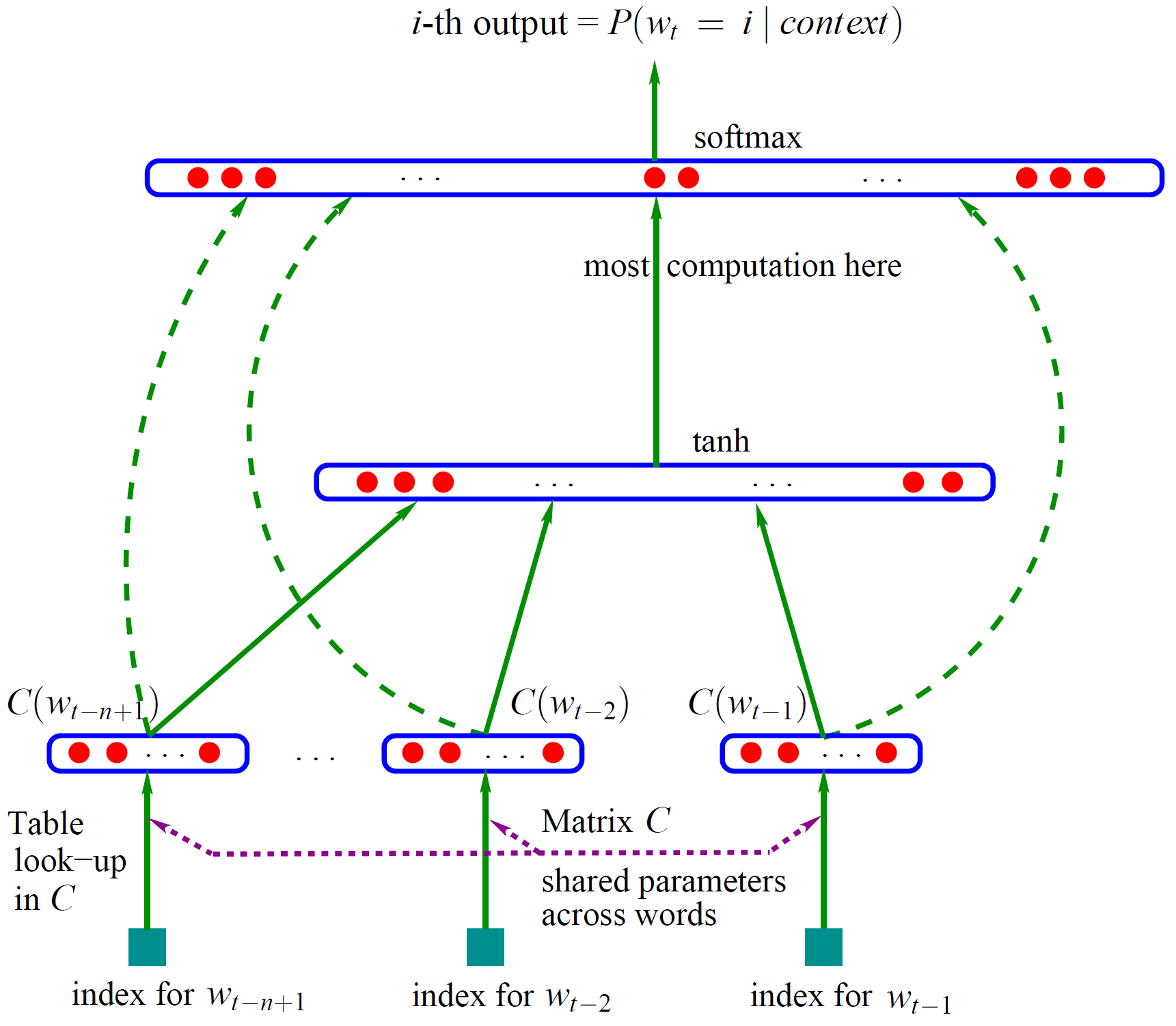
神经网络语言模型

如上图所示，其将词 $w_t$ 在训练集中的前 $n-1$ 个词的词向量 $C(w_{t-n + 1}),...,C(w_{t-2}),C(w_{t-1})$ 首尾联立起来形成输入层，隐藏层使用tanh函数并训练一个普通的神经网络，输出层在隐藏层的基础上使用softmax作为激活函数得到最后的概率值，并且这里输出层和输入层还有直连边(代表其也有参数需要训练)，其中会将词向量初始化后也进行训练，最后得到我们需要的低维词向量。

3.2、Word2Vec：

从上一个小节可以看出，需要训练的参数包括了输入层到隐藏层的参数、隐藏层到输出层的参数，其中隐藏层到输出层的参数的数量级是比较大的，而Word2Vec主要也是在这块做了优化。首先Word2Vec有两个算法模型，分别是CBOW和Skip-gram，简单来说CBOW是通过一个词 $w$ 的上下文 $Content(w)$ ，建立神经网络模型，并在训练集上最大化 $p(w\|Content(w))$ 得到参数和词向量，而Skip-gram是最大化 $p(Content(w)\|w)$ 。

再来说一下Hierarchical Softmax和Negative Sampling，这两种方法都是在简化隐藏层到输出层的网络结构。首先说一下Hierarchical Softmax，其将输出层按词在语料中的词频做成Huffman树，这样输出层到每个词的概率可以表示为一个唯一的路径，并且因为是一个二叉树，所以每个非叶子节点都可以视为一个二分类，这样输出在Huffman树中层层做分类，所以名字叫Hierarchical Softmax(层次Softmax)。

Negative Sampling其实就是一个负采样过程，通过语境 $Content(w)$ 来看，语境中的词 $w$ 就是一个正样本，其余的非 $w$ 词就是负样本，算法的优化函数是最大化正样本的概率同时最小化负样本的概率。其中负采样的作用是提高了参数训练速度(因为训练集少了)，并且负采样使用的是加权负采样(词频越高的词越容易被算作负例，即热门的没有被当做正例证明其带有更多可以学习的信息)。

Word2Vec主要的推导还请参考Hierarchical Softmax，Negative Sampling的一系列文章，讲的非常详细了。

再说回在文章引子中提到的一个Word2Vec实践，主要是参考了52nlp的中英文维基百科语料上的word2vec实验，训练集也是使用了最新的中文Wiki数据，根据52nlp的流程一路follow，最后根据用户在输入法中输入过的词的词向量，求出词向量距离最近的一些词推荐给用户，也取得了不错的效果(☺)，尤其是在处理一些基础推荐算法不能发现的隐含关系中。

参考:

1: Rumelhart D E, Hinton G E, Williams R J. Learning representations by back-propagating errors[J]. Cognitive modeling, 1988, 5(3): 1.
2： Bengio Y, Ducharme R, Vincent P, et al. A neural probabilistic language model[J]. Journal of machine learning research, 2003, 3(Feb): 1137-1155.
3: Mikolov T, Chen K, Corrado G, et al. Efficient estimation of word representations in vector space[J]. arXiv preprint arXiv:1301.3781, 2013.
4: Mikolov T, Sutskever I, Chen K, et al. Distributed representations of words and phrases and their compositionality[C]//Advances in neural information processing systems. 2013: 3111-3119.
5: Network B P. Handwritten Digit Recognition with[J]. 1989.
6: Hinton G E, Salakhutdinov R R. Replicated softmax: an undirected topic model[C]//Advances in neural information processing systems. 2009: 1607-1614.
7: Krizhevsky A, Sutskever I, Hinton G E. Imagenet classification with deep convolutional neural networks[C]//Advances in neural information processing systems. 2012: 1097-1105.
8: Lawrence S, Giles C L, Tsoi A C, et al. Face recognition: A convolutional neural-network approach[J]. IEEE transactions on neural networks, 1997, 8(1): 98-113.
9: Mikolov T, Karafiát M, Burget L, et al. Recurrent neural network based language model[C]//Interspeech. 2010, 2: 3.
10: Hochreiter S, Schmidhuber J. Long short-term memory[J]. Neural computation, 1997, 9(8): 1735-1780.
11: Werbos P J. Backpropagation through time: what it does and how to do it[J]. Proceedings of the IEEE, 1990, 78(10): 1550-1560.
12: http://deeplearning.stanford.edu/wiki/index.php/UFLDL%E6%95%99%E7%A8%8B
13: http://neuralnetworksanddeeplearning.com/index.html
14: http://www.hankcs.com/ml/back-propagation-neural-network.html
15: http://karpathy.github.io/2015/05/21/rnn-effectiveness/
16: http://www.cnblogs.com/ooon/p/5594438.html
17: http://colah.github.io/posts/2015-08-Understanding-LSTMs/
18: https://danijar.com/introduction-to-recurrent-networks-in-tensorflow/
19: https://github.com/kjw0612/awesome-rnn
20: http://www.52nlp.cn/中英文维基百科语料上的word2vec实验
21: http://licstar.net/archives/328
22: http://blog.csdn.net/zouxy09/article/details/8775360
23: http://blog.csdn.net/itplus/article/details/37969519
24: http://www.hankcs.com/nlp/word2vec.html
25： http://www.cnblogs.com/daniel-D/archive/2013/06/03/3116278.html
26： https://zh.wikipedia.org/wiki/反向传播算法#.E6.B1.82.E8.AF.AF.E5.B7.AE.E7.9A.84.E5.AF.BC.E6.95.B0