SVD、LSA(LSI)、PCA、PLSA、LDA的数学以及一个SVD的实践

本文把这些算法都放在一块讲了，而其实其中的每一个都可以来一篇长篇大论，LDA更是数据挖掘中最大的水坑(???)，但上述的算法本质都是基于SVD和LDA的，所以本文就着重在这两个问题上进行阐述，给出数学推导，并给出一些可以进一步学习的资料。剩下的算法其实就是这两个的应用，就只给出简单的应用思路。

当然，光有理论是不行的，不然就是纸上谈兵了，所以还有一个我在工作中的实施，供君参考：在搜索建议中，用户输入的前缀和最后的搜索建议是可以组成一个矩阵的(用户有点击即为1，没有点击即为0)，则根据SVD在Netflix推荐中的优异表现，则可以对用户输入前缀推荐隐含的搜索建议(注意不是给用户本身推荐，而是根据用户输入的前缀推荐)，总体来说也像是LSI(隐语义索引)，只不过LSI大部分是用于搜索结果的，数据集是某搜索引擎搜索建议的30天log数据，有用户输入的前缀，维度大致200w+，还有用户在此前缀下点击的搜素建议，维度大致300w+。算法使用的是SVD，简单说一下为什么用SVD不用LDA，LDA其实也是可以用的(-_-!)，但基于LDA文本建模的前提是将text看成word的集合，而搜索前缀和搜索建议之间并没有这种关系(尤其是在九键输入法下，用户输入的其实都是数字)。

一、先从SVD讲起

先说一下方阵，每一个方阵都可以求出其特征值λ和特征向量v，有：

$A*v=\lam*v$

特征值和特征向量的物理含义就是方阵A可以将向量v变换λ倍，且称所有的特征向量为方阵A的一组基，则该方阵可由这一组基重新表示，而特征值表示对应特征向量(基)的权重。简单的说就是特征值表示一个方阵在某方向上变化的快慢，而这个方向由特征向量建立，则在某些情况下，可以只提取特征值较大的几个特征向量，来表示原方阵。

而现实生活中大部分矩阵都不是方阵，尤其是在数据挖掘的任务中，常常都是n个用户，m个产品，或者n个词，m篇文档之类的，所以就需要引入奇异值了，假设A是M x N矩阵，U是M x M矩阵，其中U的列为 $AA^T$ 的正交特征向量，V为N x N矩阵，其中V的列为 $A^TA$ 的正交特征向量，则存在奇异值分解：

$A=U\Sigma V^T$

如图所示：

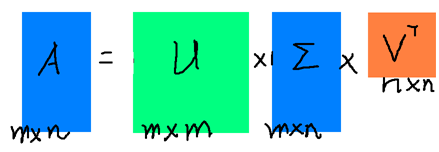
SVD分解

其中，U里面的向量称为左奇异向量，V里面的向量称为右奇异向量，Σ中除对角线外的值都是0，对角线上的值称为奇异值，且 $\Sigma_{ii}=\sqrt{\lam_i}$ ，其中 $\lam_i$ 是方阵 $AA^T$ 和 $A^TA$ 的特征值(这两个方阵的特征值相同)。奇异值的特性和特征值类似，即为矩阵在某方向上变化快慢的度量。则可取一个很小的数r，使用前r大的奇异值数量重新构造U、Σ、V，逼近原矩阵A，如图所示：

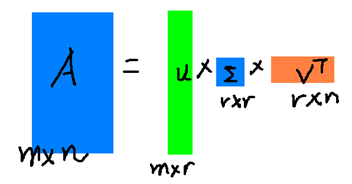
SVD取前r大的奇异值

相关理论推导可以参见We Recommend a Singular Value Decomposition，其详细的讲清楚了来龙去脉。借用吴军老师《数学之美》中的一句话，不过其表述的是SVD用在文本建模中(行是词，列是文章，后面的应用LSA中会具体说到)：“三个矩阵有非常清楚的物理含义。第一个矩阵X中的每一行表示意思相关的一类词，其中的每个非零元素表示这类词中每个词的重要性（或者说相关性），数值越大越相关。最后一个矩阵Y中的每一列表示同一主题一类文章，其中每个元素表示这类文章中每篇文章的相关性。中间的矩阵则表示类词和文章类之间的相关性。因此，我们只要对关联矩阵A进行一次奇异值分解，我们就可以同时完成了近义词分类和文章的分类。（同时得到每类文章和每类词的相关性）”。

简单的说就是把原矩阵按行列映射到更低维的空间去了，并且该低维空间是奇异值最大的一组组成(信息损失最少的一组)，则SVD有以下几种有用信息：

1、在损失最小的情况下，完成了对原矩阵的数据压缩，并且能够去掉部分噪音(奇异值小的被忽略即噪音被忽略)

2、发现隐含空间中的簇，即在去除噪音的隐含空间中，可以将一些行或列归为一类

下面来依次说明SVD的一些应用：

1、PCA(主成分分析)：

用一张图来说明吧~

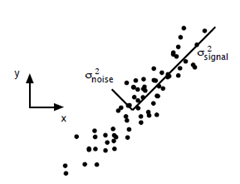
PCA示例

假设我有一些样例如上图，signal方向表示信号的方向，noise方向表示噪音的方向，则如果我用样例在x或y轴的投影来看，并不能确定信号真正的方向是什么，但如果将样例投影到图中的signal超平面，是不是信号的方向就是沿着该超平面前进的？顺便该超平面的求法是使得样例在超平面上投影的方差最大。

对于PCA来说，完成的目标是找出前r个方差最大的正交超平面，这些超平面是相互正交的，从而完成主成分分析。则SVD正好满足了PCA所需要的所有特性，奇异值最大的正好对应了变化最快的方向，则对应的奇异向量即是PCA所需要的方差最大的超平面，将奇异值最大的r个所对应的奇异向量组合起来，就是PCA完成的目标。

2、数据压缩：

从SVD最后的那个图就可以明显的看出来了，只需要m*r+r*r+r*n的空间就可以近似的表示m*n的空间，各位可以自己算算压缩率。再提一点，曾经在上研究生的时候做过一次NMF(非负矩阵分解)，当初看的论文已经全部忘记了(☺)。搞NMF的原因是大矩阵在我的破电脑上内存装不下，其思路也类似，将原矩阵分解成3个矩阵相乘(我的破电脑就装下了)，当时是对这些NMF后的数据进行了一个分类的工作，我很清楚的记得NMF后的分类正确率是比在原始矩阵上直接分类正确率要低的，所以一段时间内我对矩阵分解唾弃不已，直到后来的Netflix推荐系统大赛，我只能说“是在下输了”，这里按下不表，见下文。

3、LSA、LSI：

用Introduction to Latent Semantic Analysis中的例子来说明，有如下的单词到文档矩阵A：

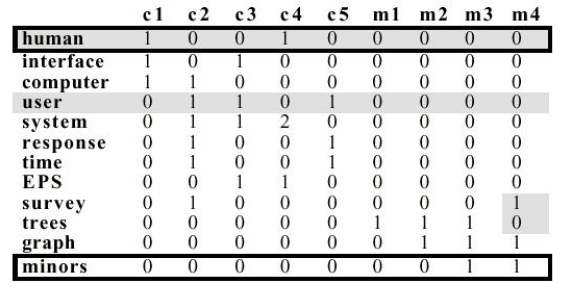
word_text矩阵

对其进行SVD，则得到的三个矩阵为U、Σ、V，分别表示为：

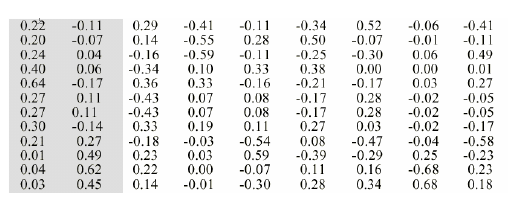SVD分解后U 矩阵U

SVD分解后Σ 矩阵Σ

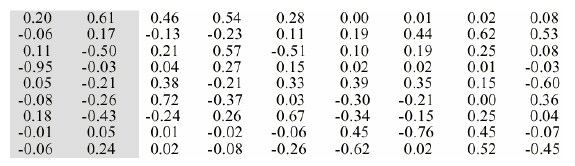SVD分解后V 矩阵V

则取前两个最大的奇异值，并将新的U’，Σ’，V’重新乘起来可得新的矩阵A’：

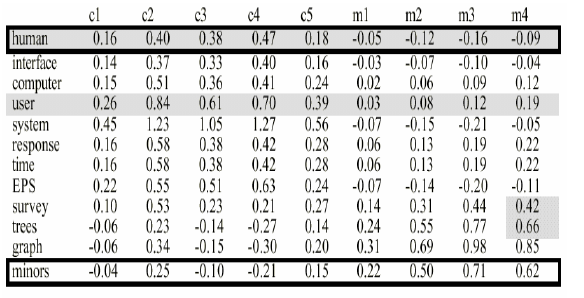
SVD分解后新的A'

这样，所有为0的值都被重新填充了，也就是发现了隐语义(其实本质是将单词和文档都映射到同一个去除噪音的低维空间上，再在该空间求距离，这个空间可以称为隐语义)，那我新来一篇文档，只要对其分词之后，按该文档的词向量乘以SVD后的矩阵，就可以得到新文档与其他文档的相似度，从而给出最相似的文档，也就是基于隐语义得到的相似文档，即Latent Semantic Analysis(Index)。

4、应用于推荐：

和上面的LSA思路类似，推荐系统也有类似的一个user-item矩阵，矩阵中的值表示用户对该产品的打分。算法先对矩阵中所有为0的值填充一个中数值(比如1-5的打分则对应3)，再对填充后的矩阵进行SVD，再取前r大的奇异值，再重新乘起来，得到的新矩阵中的数值便是预测的user对item的打分。这样的打分是在隐含空间中，发现user和item的簇，比起一般的CF或者content recommendation，效果都会好一些，所以火了好一阵。

然而在Netflix的比赛中，由于数据的维度大幅增加，而SVD的复杂度又是O(n³)，故又产生了一些只计算user-item矩阵中不为0值的伪SVD算法，例如SVD++等，后来推荐系统的热点又往LDA、word2vec方向发展，不过这都是后话了，具体的可以参见项亮写的一篇文章关于LDA, pLSA, SVD, Word2Vec的一些看法。

二、PLSA、LDA

为了说清楚PLSA以及LDA，而算法都有一个产生的历史沿革，所以还是从文本建模开始说起吧。文本建模本质是基于统计的(使用训练集的统计去估计参数)，而统计学则是猜测上帝的游戏，感觉刁刁的有没有。

那如何去猜测文本建模中的这个上帝呢？就需要先引入N-gram语言模型，对于一篇词序列(文章)： $S=w_1w_2w_3\cdots w_m$ ，其中S代表文章，w代表每一个词，则该篇文章出现的概率可以定义为： $P(S)=P(w_1w_2\cdots w_m)=P(w_1)\cdot P(w_2\|w_1)\cdots P(w_m\|w_1w_2\cdots w_{m-1})=\prod_{i=1}^mP(w_i\|w_{i-n+1},\cdots ,w_{i-1})$

简单的说N-gram认为文章中后一个词的出现是建立在前面的词出现的概率之上的(也符合写文章的逻辑，即后面的内容与前面的有关)，那完美的N-gram就是在上式的 $n=m$ 的时候，然而这样参数非常多不好计算，故产生了unigram、bigram、trigram，即n分别取1、2、3。顺道提一句N-gram也称为n-1阶马尔科夫模型，而马尔科夫链的一个性质就是这一次发生的概率只和前一次的转移概率有关。

以unigram model说起：其认为上帝拥有一个词典的骰子，这个词典包括了能见到的所有词，那上帝每次都抛这个骰子，从而最后产生一篇文本，当然骰子的每一面(每个词)出现的概率不同，算法所做的工作就是估计这些词出现的概率 $\vec{p}$ 。这是最简单的模型，也称为词袋模型。当然这个模型隐含着每个词的出现都是独立的，所以每个词出现的次数服从多项分布(二项分布扔硬币游戏在多维上的扩展) $w\sim Mult(w\|\vec{p})$ ，如图所示：

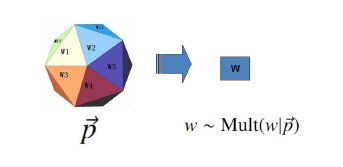
unigram

unigram使用MLE就可以解，就不多提了，下面还要引申一个概念(足见LDA的复杂性，码了半天字只是铺垫…的一部分☺)，unigram是属于概率学中的频率学派，即只根据事件发生的频次来做参数估计，而还有一个学派叫做贝叶斯学派(北少林，南武当？？？北北邮，南华科？？？)，其根据一些先验知识来做参数估计，该学派认为参数的参数也应该是一个随机变量。两种学派的区别可以参见贝叶斯学派与频率学派有何不同？然后贝叶斯的学者们就把unigram改造了一下，如图所示：

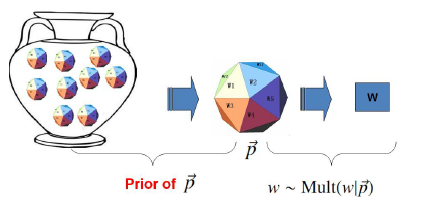
贝叶斯unigram

这次上帝有了一个坛子，其中装满了词的骰子，上帝首先从坛子中拿了一个骰子，然后使用这个骰子不停的抛掷，得到一篇文章。其中坛子里的骰子 $\vec{p}$ 服从一个概率分布 $p(\vec{p})$ ，则这个分布称为先验分布(先验知识)。上面讨论了，我们已经知道 $\vec{p}$ 服从一个多项分布，那其先验分布 $p(\vec{p})$ 则是狄利克雷分布，狄利克雷分布简单说就是M个多项分布的坛子中每一个的出现概率的分布，即观测到的事件概率的概率，具体的我就不解释了，因为涉及的知识点实在太多，需要从Gamma函数讲起(主要我也不是数学专业，啃起这一大坨也很吃力。。。)，各位感兴趣可以参见腾讯广点通组靳志辉的一篇《LDA数学八卦》，写的非常好。还有一点需要提一下，狄利克雷先验分布 + 多项分布 ——> 狄利克雷后验分布，可以通过该推论直接求参数估计。

写了这么多终于到了本节的主角之一PLSA了，随着时间的发展文本建模的模型也在优化，在前面讲过的SVD应用LSA中，分解的小矩阵Σ可以理解其物理意义为隐含的语义层(主题层)，即一个词可以有多个主题，一篇文章也可以有多个主题，那将一篇文章有多个主题的思想应用到unigram的上帝扔骰子例子中有：

上帝有两种骰子，一种对应了文章-主题的骰子，每一面是主题的编号，从1到K；另一种是主题-词的骰子，共K个，每一面即是选定主题下的N个词。上帝先定下文章-主题骰子的K个面，然后重复以下过程直到文章生成完毕：投掷该文章-主题的骰子，得到一个主题z；再投掷对应主题z的主题-词的骰子，得到对应的词。如图表示：

PLSA

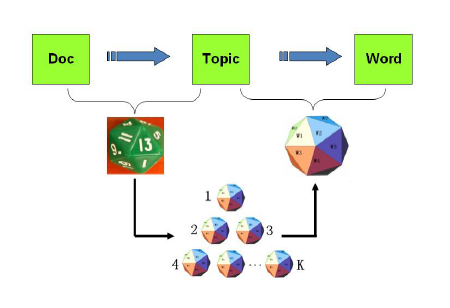
PLSA相关可以参考Hoffman的那篇著名paper[6]，求解方式为EM算法。当然算法讲到这里，贝叶斯学派又来了，他们觉得在上面的PLSA中，文章-主题的分布和主题-词的分布都是已知的，这不科学，所有的变量都应该是未知的。故他们将PLSA又改造了一下，在上面两个已知的分布前加入了一些先验，这个先验分布使用的也是狄利克雷分布，那就引出了本文的另一个主角LDA(隐狄利克雷分布)了，如图所示：

LDA

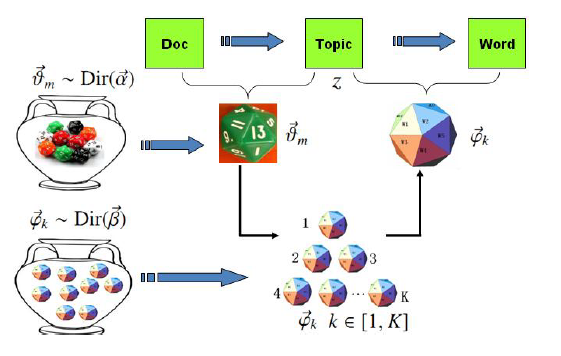
现在的上帝拥有两个大坛子，一个坛子装满了文章-主题的骰子，另一个装满了主题-词的骰子，两个坛子中的骰子都满足狄利克雷分布。上帝首先从主题-词的坛子中独立抽取K个骰子，编号从1到K，然后从文章-主题的坛子中随机抽取一个文章-主题的骰子，该骰子共K个面，然后重复以下过程直到文章生成完毕：投掷该文章-主题的骰子，得到一个主题z；再投掷对应主题z的主题-词的骰子，得到对应的词。

而在该LDA模型中，其实是隐含着两个狄利克雷+多项共轭分布的，一个是文章-主题的，一个是主题-词的，所以该算法名为隐狄利克雷分布。我记得在哪里看过一个盲人摸象的比喻，感觉很适合用来形容LDA，如图：

盲人摸象

象就是一篇文章，每个人摸到的就是一类主题的词，而一篇文章会有多个主题，这些主题都可以用来形容这篇文章。这样是不是更容易理解一些？

在对LDA的求解中，使用的是Gibbs采样，而Gibbs采样是一个特殊的MCMC(马尔科夫蒙特卡洛)过程。简单来说主要是使用了马尔科夫链转移矩阵的收敛定理，通过不断的采样修正的方式，得到收敛的转移概率矩阵，该矩阵也正好是关于主题-词和文章-主题的概率分布，即我们需要求解的参数估计。这一大坨的数学也很多，需要了解马尔科夫链、统计模拟、以及马氏链稳定性带来的采样方式等，具体的还请参见《LDA数学八卦》，中文资料里面我觉得是讲LDA讲得最好的了，我就不详细赘述了(太吃数学，深感无力。。。)。

最后说一下LDA的应用吧，实际上LDA的结果是求得一个关于主题-词的分布(当然还有一个文章-主题的分布，不过该分布是关于训练集的，所以一般不使用)，即可以用该分布来分析语义的隐含主题。在工业界中，LDA一般是用来将语义分析到主题维度，并将其主题作为算法的一个弱特征使用，而将主题作为强特征来使用一般的效果都不太理想。

前言提过了，将本文的这些算法放在一块讲的原因。具体来说其实就是LDA和SVD两个算法，而且他们的目的都是发现样本中的隐含层。SVD是基于矩阵分解，LDA是假设了文本建模的一个过程，其余的算法几乎都是在这两个算法上的扩展，隐含模型这一块可以做的事情还是很多的，可以说是百花齐放吧，也是deep learning之前最火的模型了。

参考:

1: Deerwester S, Dumais S T, Furnas G W, et al. Indexing by latent semantic analysis[J]. Journal of the American society for information science, 1990, 41(6): 391.
2: Schütze H. Introduction to Information Retrieval[C]//Proceedings of the international communication of association for computing machinery conference. 2008.
3: Koren Y, Bell R, Volinsky C. Matrix factorization techniques for recommender systems[J]. Computer, 2009, 42(8): 30-37. MLA
4: http://code.google.com/p/lsa-lda/
5: http://www.ams.org/samplings/feature-column/fcarc-svd
6: Hofmann T. Probabilistic latent semantic indexing[C]//Proceedings of the 22nd annual international ACM SIGIR conference on Research and development in information retrieval. ACM, 1999: 50-57.
7: Blei D M, Ng A Y, Jordan M I. Latent dirichlet allocation[J]. Journal of machine Learning research, 2003, 3(Jan): 993-1022.
8: Zhai C X. A note on the expectation-maximization (em) algorithm[J]. Course note of CS410, 2007.
9: http://www.cs.princeton.edu/~blei/lda-c/
10: Heinrich G. Parameter estimation for text analysis[J]. University of Leipzig, Tech. Rep, 2008.
11: Hofmann T. Unsupervised learning by probabilistic latent semantic analysis[J]. Machine learning, 2001, 42(1-2): 177-196.
12: 《LDA数学八卦》